|
不等式的解法
一、一元二次不等式的解法
一元二次不等式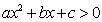 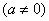 ,其中 ,其中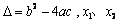 是方程 是方程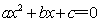 的两个根且 的两个根且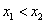 ,则不等式的解集如下: ,则不等式的解集如下:
当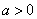 时,解集 时,解集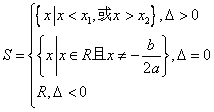
当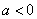 时,解集 时,解集
二、一元高次不等式的解法
一元高次不等式通常进行因式分解,化为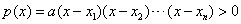 (或<0)的形式,然后利用穿根法求解,利用此法时注意将x的系数化为正的,以防出错. (或<0)的形式,然后利用穿根法求解,利用此法时注意将x的系数化为正的,以防出错.
穿根法求解步骤:①将p(x)的最高次项的系数化为正数;②将p(x)分解因式,化成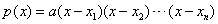 (取 (取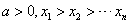 )③当 )③当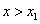 时,所有因式皆正,积为正;当 时,所有因式皆正,积为正;当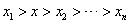 时,有一个因式为负,其余为正,积为负,依次类推;④当相应的方程有偶次重根时,遵循“奇穿偶不穿”的规则。 时,有一个因式为负,其余为正,积为负,依次类推;④当相应的方程有偶次重根时,遵循“奇穿偶不穿”的规则。
三、分式不等式的解法
分式不等式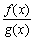 >0(或<0)的求解可应用同解原理,转化为整式不等式求解. >0(或<0)的求解可应用同解原理,转化为整式不等式求解.
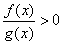 (<0) (<0)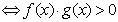 (<0); (<0);
 (≤0) (≤0)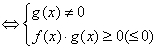
|

