|
直线与直线的位置关系
(1)位置关系:空间两条直线有三种位置关系:
空间中直线与直线的位置关系如下图:

(2)公理4:
①叙述:平行于同一条直线的两条直线互相平行。
②符号表示: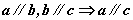 。 。
③作用:平行线的传递性作用,是判断或证明空间两条直线平行的依据。
公理4表明空间中平行于一条已知直线的所有直线都互相平行,它给出了判断两条直线平行的依据。
经过直线外一点,有且只有一条直线和这条直线平行。
证明空间两条直线平行的方法:
方法1:利用定义
用定义证明两条直线平行,须证两件事:一是两直线在同一平面内;二是两直线没有公共点。
方法2:利用公理4
用公理4证明两条直线平行,只须证一件事:就是须找到直线c,使得 ,同时 ,同时 ,由公理4,得到 ,由公理4,得到 . .
(3)等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
推论1:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。
推论2:如果一个角的两边与另一个角的两边分别平行,那么这两组直线所成的角相等或互补。
(4)异面直线:
①异面直线的定义:指不同在任何一个平面内的两条直线。
②异面直线的画法:作图时通常用一个或两个平面衬托。如图:

③异面直线的判定:本教材没有异面直线的判定定理,一般用反证法证明。
④异面直线所成的角:
Ⅰ、定义:如图所示,已知两条异面直线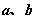 ,经过空间任一点O作直线 ,经过空间任一点O作直线 , , ,我们把 ,我们把 与 与 所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)。 所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)。

两条异面直线所成角的范围是(0°,90°]。
如果两条异面直线所成的角是直角,那么我们就说这两条异面直线互相垂直。两条互相垂直的异面直线a,b,记作 . .
Ⅱ、定义的实质:空间异面直线所成角化归转化为平面内两直线所成角来表示,体现了空间归面的思想方法。
Ⅲ、异面直线所成角的求法:平移归面法;向量法。
IV、两异面直线所成的角注意:
(1)两异面直线所成的角与点O的选取无关。
(2)两异面直线所成角θ的范围是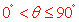 . .
(3)判定空间两条直线是异面直线的方法:
①判定定理:平面外一点A与平面内一点B连成的直线与平面内不过点B的直线是异面直线。
②反证法:证明两直线共面不可能。
|

