|
空间几何体的表面积
(1)求空间几何体表面积的方法:沿多面体的棱或旋转体的母线剪开,把它们展成平面图形,利用平面图形求面积的方法,求立体图形的表面积。将空间图形问题转化为平面图形问题,是解决立体几何问题基本的、常用的方法。
(2)具体步骤:先求侧面积,再求全面积。
①棱柱、棱锥、棱台的侧面积:
棱柱的侧面展开图是平行四边形;棱锥的侧面展开图是由多个三角形拼接成的;棱台的侧面展开图是由多个梯形拼接成的。按照平面几何的三角形、梯形、平行四边形的面积计算公式计算它们的侧面积。
②圆柱、圆锥、圆台的侧面积:
⑴圆柱侧面积:圆柱的侧面展开图是一个矩形。如果圆柱的底面半径为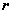 ,母线长 ,母线长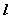 ,那么圆柱的侧面面积为 ,那么圆柱的侧面面积为 。因此,圆柱的表面积 。因此,圆柱的表面积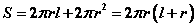 。 。
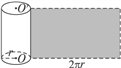
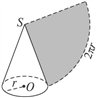
⑵圆锥侧面积:圆锥的侧面展开图是一个扇形。如果圆锥的底面半径为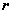 ,母线长为 ,母线长为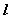 ,那么圆锥的侧面积为 ,那么圆锥的侧面积为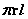 。因此,圆锥的表面积 。因此,圆锥的表面积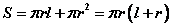 。 。
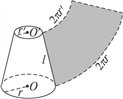
⑶圆台侧面积:圆台的侧面展开图是一个扇环。如果圆台的上下底的半径分别为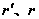 ,母线长为 ,母线长为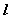 ,那么圆台的侧面积为 ,那么圆台的侧面积为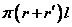 。因此,圆台的表面积等于上、下两个底面的面积和加上侧面的面积,即 。因此,圆台的表面积等于上、下两个底面的面积和加上侧面的面积,即
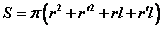 。 。
⑷圆柱、圆锥、圆台侧面积的关系:
圆柱和圆锥都可以看作是圆台退化而成的几何体。圆柱可以看作是上下底面全等的圆台,圆锥可看作是上底面退化成一点的圆台,于是:
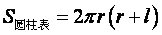
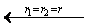
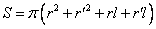
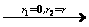
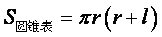
即圆柱和圆锥的侧面积公式都可以看作由圆台侧面积公式演变而来。
|

