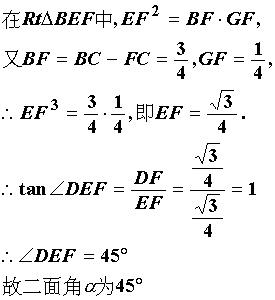23.本小题考查空间线面关系,正棱柱的性质,空间想象能力和逻辑推理能力.
(1)证明:　∵a₁b₁c₁-abc是正三棱柱,
∴四边形b₁bcc₁是矩形.连结b₁c,

交bc₁于e,则b₁e=ec.连结de.
在△ab₁c中,∵ad=dc,　∴de∥ab₁,

∴ab₁∥平面dbc₁.
(2)解:作df⊥bc,垂足为f,

则df⊥面b₁bcc₁,

连结ef,则ef是ed在平面b₁bcc₁上的射影.
∵ab₁⊥bc₁,　由(1)知ab₁∥de,　∴de∥bc₁,
则bc₁⊥ef,　∴∠def是二面角α的平面角.
设ac=1,则dc=　∵△abc是正三角形,
  

取bc中点g.　∵eb=ec,　∴eg⊥bc.