(26)本小题主要考查空间图形的线面关系、三棱柱的性质、

空间想象能力和逻辑推理能力。

　　解：(Ⅰ)l∥a₁c₁。证明如下：

根据棱柱的定义知平面a₁b₁c₁和平面abc平行。

　　　　由题设知直线a₁c₁=平面a₁b₁c₁∩平面a₁bc₁，

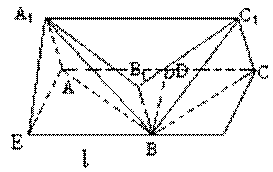直线l=平面a₁bc₁∩平面abc。

　　根据两平面平行的性质定理有l∥a₁c₁。　　　　　　　　　　　　　　　　　　　

　　(Ⅱ)解法一：

过点a₁作a₁e⊥l于e，

则a₁e的长为点a₁到l的距离。

连结ae。

由直棱柱的定义知a₁a⊥平面abc。

　　∴直线ae是直线a₁e在平面abc上的射影。

　　又l在平面abc上，根据三垂线定理的逆定理有：ae⊥l。

　　由棱柱的定义知a₁c₁∥ac，又l∥a₁c₁，

　　∴l∥ac。

　　作bd⊥ac于d，则bd是rt△abc斜边ac上的高，且bd=ae，

　　从而，

　　在rt△a₁ae中，　∴a₁a=1，∠a₁ae=90°，

　　∵，

　　故a₁到直线的距离为。

　　解法二：

　　同解法一得l∥ac。

由平行直线的性质定理知∠cab=∠abe，

从而有rt△abc∽rt△bea，ae：bc=ab：ac，

　　以下同解法一。