六、本题考查直线方程、两点间的距离公式、参数方程以及轨迹方程的求法.


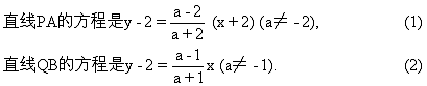
![]()
2.当a≠0时,直线pa与qb相交,设交点为m(x,y),由(2)式得
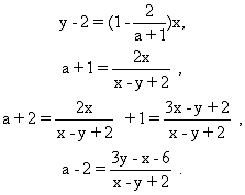
将上述两式代入(1)式,得
![]()
整理得 x2-y2+2x-2y+8=0, (*)
![]()
当a=-2或a=-1时,直线pa和qb仍然相交,并且交点坐标也满足(*)式.
所以(*)式即为所求动点的轨迹方程.
解法二:设直线pa和qb的交点为m(x,y).
当点m与点p及点q都不重合时,直线pm的方程是
(x+2)(y-2)=(y-2)(x+2),
直线qm的方程是
x(y-2)=(y-2)x.
由方程组
![]()
解得直线pm和直线l的交点a的坐标为
![]()
由方程组
![]()
解得直线qm和直线l的交点b的坐标为

根据题意,线段ab两端点a,b的横坐标有如下关系:
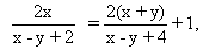
从而得 x2-y2+2x-2y+8=0,(*)即
![]()
又因点m与点p或点q重合时,m点的坐标也满足(*)式.所以(*)式即为所求动点m的轨迹方程.