|
一、考纲展示 1、理解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题. 2、了解数列极限和函数极限的概念. 3、掌握极限的四则运算法则;会求某些数列与函数的极限. 4、了解函数连续的意义,理解闭区间上连续函数有最大值和最小值的性质. 5、了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念. 6、熟记基本导数公式.掌握两个函数和、差、商的求导法则.了解复合函数的求导法则.会求某些简单函数的导数. 7、理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值. |
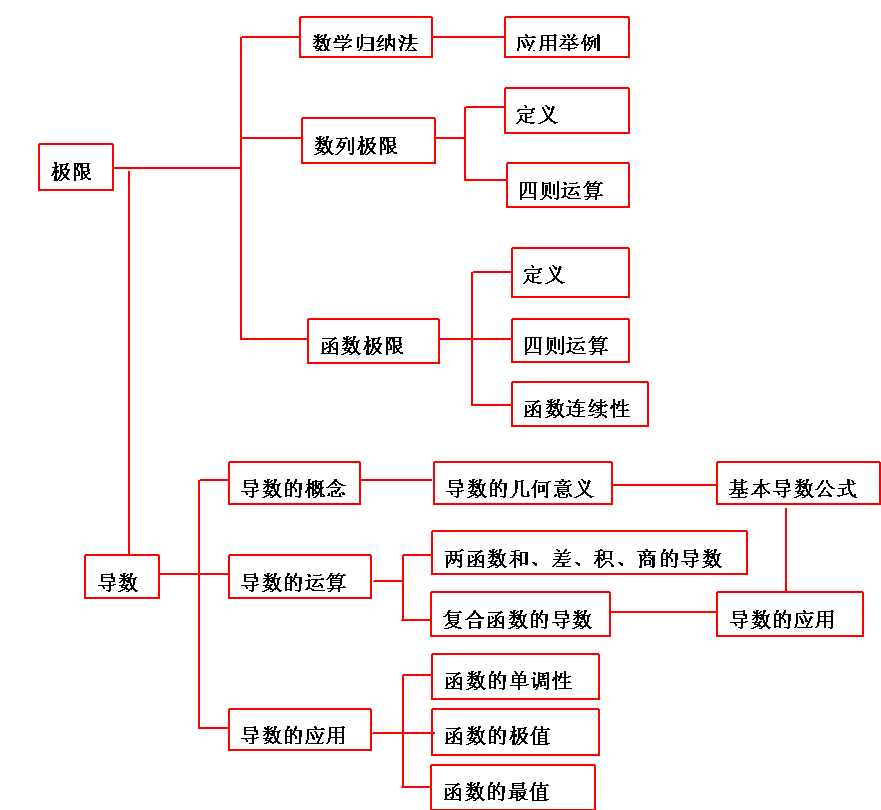
| 专题结构
|
|
命题特点 数列的极限在中学数学与高等数学中起着衔接作用,因而它是高考常考内容,多以选择、填空题形式出现,也渗透到解答题中,命题方向逐步由用定义求极限,直接用极限的四则运算法则求极限这些单一考查方面向结合等差、等比数列的计算求极限,结合数列求和法求极限等一些综合考查过渡.函数极限是另一个高考热点,函数在无穷远处的极限,类似于数列的极限,而在`x=x_0`处的极限,计算它时有独特方法,比如`x=x_0`不在`f(x)`定义域时,往往先采用去零因子(约分)方法,再求极限,对于较为复杂的函数极限计算,可借助于函数极限的四则运算法则处理. 通过观察、分析等手段利用不完全归纳法得出一个结论,再用数学归纳法去证明该结论也是高考常见题型之一,这里归纳、猜想、证明是不完全归纳法与完全归纳法的综合应用. 高考对导数的考查定位于作为解决初等数学问题的工具出现,侧重于考查导数在函数与解析几何中的应用,主要有以下三个方面: ①运用导数的有关知识,研究函数最值问题,这一直是高考常考不衰的热点内容.另一方面,从数学角度反映实际问题,建立数学模型,转化为函数的最大值与最小值问题,再利用函数的导数,顺利地解决函数的最大值与最小值问题.从而进一步地解决实际问题. ②利用导数的几何意义,研究曲线的切线斜率是导数的一个重要应用,并且也是高考考查的重点内容之一.函数`y=f(x)`在`x=x_0`处的导数,表示曲线在点`P(x_0,f(x_0))`处的切线斜率. ③运用导数的有关知识,研究函数的单调性是导数的又一重点应用,在高考中占主导地位. |
| 考点案例 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高) 一、导数的基本问题 1、求下列函数的导数 (1)`y=1/x^2` (2)`y=1/sinx` (3)`y=1/x+2/x^2+1/x^3` (4)`y=sinx/x`
二、函数的单调性 1、(2006年高考山东卷)设函数`f(x)=ax-(a+1)ln(x+1),其中a>=-1,求f(x)`的单调区间.
三、函数的极值与最值 1、(2006年高考福建卷)已知函数`f(x)=-x^2+8x,g(x)=6lnx+m` (1)求`f(x)在区间[t,t+1]上的最大值h(t)`; (2)是否存在实数`m,使得y=f(x)的图象与y=g(x)`的图象有且只有三个不同的交点?若存在,求出`m`的取值范围;若不存在,说明理由.
|
|
|
方法感悟 1、导数概念 函数`f(x)在x=x_0`处的导数f'`(x_0)`的实质是增量之比的极限,但在计算中只取它的应用含义,f'`(x_0)`是函数f(x)的导函数f'(x)当`x=x_0`时的函数值. 若`y=f(x)在x_0`处可导,则 `lim_(Delta x rarr 0)(f(x_0+a Delta x)-(x_0+b Delta x))/ (Delta x)=alim_(Delta x rarr 0)(f(x_0+a Delta x)-f(x_0))/(a Delta x)-blim_(Delta x rarr 0)(f(x_0+bDelta x)-f(x_0))/(bDelta x)=af'``(x_0)`-bf'`(x_0)`=(a-b)f'`(x_0)`(其中`a•b!=0)`. 函数`y=f(x)在点x_0处的导数几何意义:指曲线y=f(x)在点(x_0,f(x_0))`处的切线的斜率,即f'`(x_0)`=`k_切`,此切线方程为:y-f`(x_0)`=f'`(x_0)(x-x_0)`处. 2、导数应用 (1)在运用导数判定函数单调性时,应注意`f'(x)>0`是`f(x)`递增的充分条件而非必要条件,(同样`f'(x)<0`亦如此),再求单调区间时,应先确定定义域,然后再根据`f'(x)>0`(或`f'(x)<0`)解出定义域内相应x的范围. (2)对于函数的极值来说,`f'(x_0)=0`是该点为极值点的必要条件,而非充分条件,只有在`x_0`左右两侧`f'(x)`异号时,`f(x_0)`才是极值;极值点是区间内部的点,不会是端点,若`f(x)`在`(a,b)`内有极值,那么`f(x)在(a、b)`内决不是单调函数;极大值与极小值没有必然的大小关系:一般情况下,当函数`f(x)在[a,b]`上连续且有有限个极值点时,函数`f(x)在[a,b]`内极大值和极小值交替出现. (3)在`[a,b]`上连续的函数`f(x)`在`[a,b]`上必有最大值和最小值,设函数`f(x)`在`[a,b]`上连续,在`(a,b)`内可导,求`f(x)`在`[a,b]`上的最值步骤如下: ①求`f(x)`在`(a,b)`内的极值; ②求得`f(x)`的各极值与`f(a)、f(b)`比较,其中最大的一个是最大值,最小的一个是最小值. |