第六章  不等式
 §6.1 不等式的性质与解法

考纲展示 专题结构 命题特点 考点案例 考能训练 方法感悟
    一、考纲展示
    1、理解不等式的性质及证明．
     2、掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用．
     3、掌握分析法、综合法、比较法证明简单的不等式．
     4、掌握简单不等式的解法．
     5、理解不等式`|a|-|b|<=|a+b|<=|a|+|b|`．
    专题结构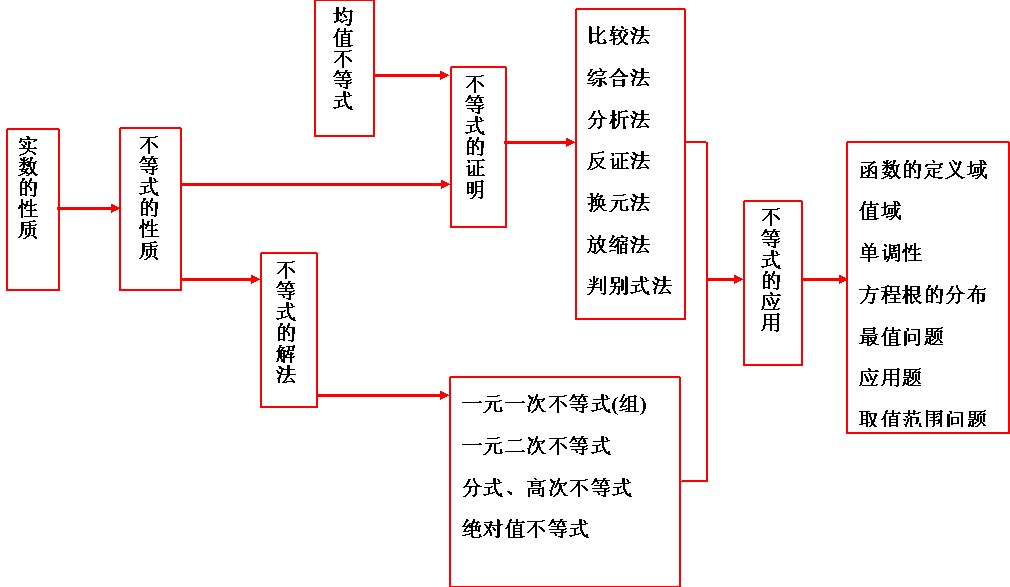   
    命题特点
    本章知识点虽然较少，但综合性较强，难度也比较大，在历年高考试题中有较大的比重，约占总分的20﹪左右，远远高于课时中的比例，从题型看，有关不等式的试题近几年各是一道选择题或填空题，一道解答题，文科题多为解不等式，理科以证明不等式为多，从近几年试卷上看，文科在不等式证明上的要求比理科低，其他考题中有些还要用到有关不等式的知识．单独考不等式的考题占分不多，但涉及不等式的知识、方法、技巧的问题往往占有较大的比例，其中不等式常常与下列知识相结合考查：
     (1)不等式性质的考查常与指数函数、对数函数、三角函数性质的考查相结合，一般多以选择题的形式出现，有时也与充要条件、函数单调性等知识结合，且试题难度不大；
     (2)解不等式的试题主要在解答题中出现，常常是解含参不等式较多，且多与二次函数、指数、对数，可能还会出现导数相结合命题；
     (3)证明不等式是理科考查的重点，经常同一次函数、二次函数、数列、解析几何，甚至还可能与平面向量结合起来考查．

    考点案例
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)

    一、不等式的概念与性质
     1、判断下列命题的真假，并说明理由
     (1)`a>b rArr ac^2>bc^2;`
     (2)`a/c^2>b/c^2 rArr a>b`;
     (3)`a>b,ab!=0 rArr 1/a<1/b`；
     (4)`a>b,c<d,cd<0 rArr a/c>b/d`；
     (5)`a^4>b^4 rArr |a|>|b|`．

    提示 示范 　
    二、一元一次与一元二次不等式
     1、(2006年潍坊模拟)已知`f(x)=-3x^2+a(6-a)x+b`．
     (1)解关于`a的不等式f(1)>0`；
     (2)当不等式`f(x)>0的解集为(-1,3)时，求实数a、b`的值．
    提示 示范 　

    三、高次不等式与分式不等式
     1、解关于`x的不等式：x/(x-1)<1-a`
    提示 示范 　

    四、含绝对值不等式
     1、(2005年高考浙江卷)已知函数`f(x)和g(x)`的图象关于原点对称，且`f(x)=x^2+2x`
     (1)求函数`g(x)`的解析式；
     (2)解不等式`g(x)>=f(x)-|x-1|`．
    提示 示范 　

  
    　 　

    考能训练
    参考答案

 
    方法感悟
    1、不等式的性质是解(证)不等式的基础，对任意两实数a、b，有`a-b>0 hArr a>b`;`a-b=0 hArr a=b`; `a-b<0 hArr a<b`．这是比较两数大小的理论依据，也是学习不等式的基础．
     2、对于不等式的性质，关键是正确理解和运用，要弄清每一个性质的条件和结论，注意条件的加强或减弱、条件与结论之间的相互联系．
     3、不等式的性质应用于证明不等式，往往是从条件推出结论的变换关系，而解不等式则要求等价变形．
     4、判断不等式是否成立，常利用不等式的基本性质、函数的单调性和特殊值等方法．
     5、由`a<f_1(x_1,y_1)<b,c<f_2(x_1,y_1)<d，求g(x_1,y_1)`的取值范围，可利用待定系数法解决．设`g(x_1,y_1)=pf_1(x_1,y_1)+qf_2(x_1,y_1)`，用恒等变形待定系数`p，q，可求到g(x_1,y_1)`的取值范围．
     6、解决含有绝对值不等式问题的基本思想是设法去掉绝对值符号，化归为不含绝对值符号的不等式去解．脱去绝对值符号的方法主要有：公式法(即利用公式`|x|<=a(a>0) hArr –a<=x<=a,|x|>=a(a>0) hArr x<=-a或x>=a`)、分段讨论法、平方法、几何法等．这几种方法应用时各有利弊，在解只含有一个绝对值的不等式时，用公式法较为简便；但若不等式含有多个绝对值时，则应采用分段讨论法；应用平方法时，要注意只有在不等式两边均为非负的情况下才能施行．因此，我们在去绝对值符号时，用何种方法需视具体情况而定．

返回

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。