|
一、考纲展示 1.理解任意角的概念、弧度的意义,能正确地进行弧度与角度的换算. 2.掌握任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义.掌握同角三角函数的基本关系式: `sin^2alpha+cos^2alpha=1`,`sinalpha/cosalpha=tanalpha`,`tanalphacotalpha=1` 掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义.了解奇函数、偶函数的意义. 3.掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式. 4.能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明. 5.了解正弦函数、余弦函数、正切函数的图象和性质,会用“五点法”画正弦函数、余弦函数和函数`y=Asin(omegax+varphi)`的简图,理解`A、omega、varphi`的物理意义. 6.会用已知三角函数值求角,并会用符号`arcsinx、arccosx、arctanx`表示. 7.掌握正弦定理、余弦定理,并能初步运用它们解斜三角形,能利用计算器解决解三角形的计算问题. |
专题结构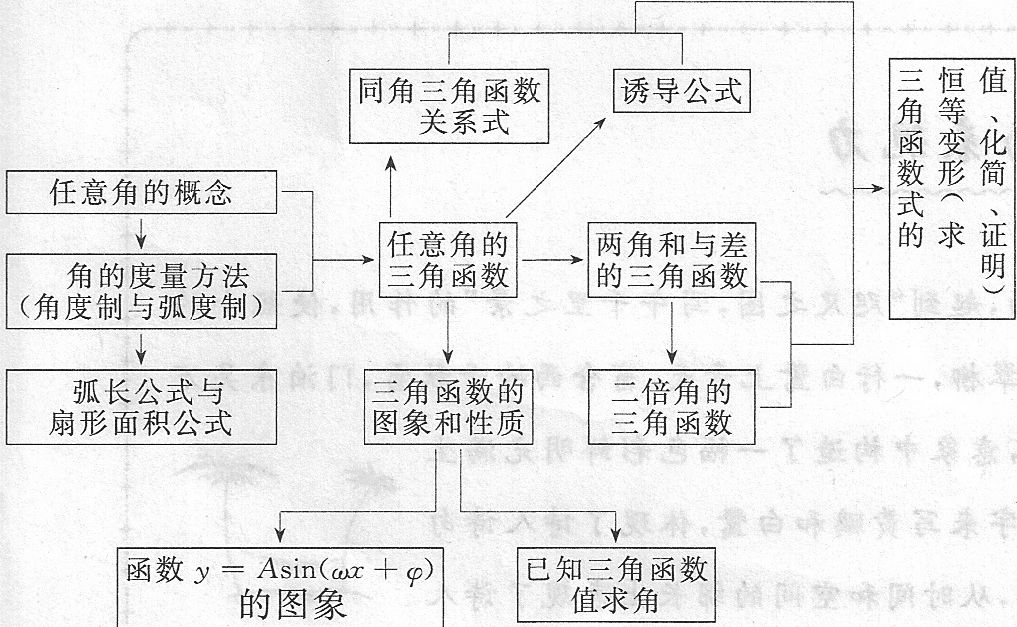 . |
|
命题特点 三角函数是中学中重要的基本初等函数之一,它的定义和性质有十分明显的特征和规律性,它和代数、几何有着密切的联系,是研究其他部分知识的重要工具,在实际问题中也有着极广泛的应用,因而是高考对基础知识和基本技能考查的重要内容之一.从近年高考,特别是2006年高考来分析,考查本章内容的形式与特点是: (1)在考查三角函数的图象和性质时多以选择题、填空题形式出现,如2006年全国卷(I)第6题,全国卷(Ⅱ)第2题,这些题已经淡化了特殊技巧,讲究通性通法,难度属中低档.重在基础知识考查,但有时也以解答题形式出现,如2006年重庆、广东、上海等考卷中出现了这种形式. (2)利用三角公式求值题每年必考,且试题有一定的难度,注重对基本公式、恒等式以及变形式的考查,突出数学思维方法.如2006年湖南卷第17题,安徽卷第17题. (3)三角函数的值域、最值、单调性是考查的重点对象,是三角解答题的主要题型.这类试题往往概念性强,具有一定的综合性和灵活性,顺利解答有一定的难度,如2006年山东卷第17题,辽宁卷第17题. |
| 考点案例 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高) 1、已知角`beta`的终边与函数`y=-2|x|`的图象重合,求`sinbeta和cosbeta`的值.
2、(2006年高考安徽卷)已知`(3pi)/4<alpha<pi`,`tanalpha+cotalpha=-10/3`. (1)求`tanalpha`的值; (2)求`(5sin^2(alpha/2)+8sin(alpha/2)cos(alpha/2)+11cos^2(alpha/2)-8)/(sqrt(2)(alpha-pi/2))`.
3、(2005年高考天津卷)已知`sin(alpha-pi/4)=7sqrt(2)/10`等等,`cos2alpha=7/25`.求`sinalpha`及`tan(alpha+pi/3)`.
4、(2005全国高考Ⅱ19)`△ABC`中,内角`A,_B,C`的对边分别为`a,b,c`.已知`a,b,c`成等比数列,且`cosB=4/3`. (1)求`cotA+cotC`的值, (2)设`vec(BA)*vec(BC)=3/2`,求`a+c`的值
5、(2004浙江高考理17)在`△ABC`中,角`A、B、C`所对的边分别为`a、b、c`,且`cosA=1/3`. (1)求`sin^2((B+C)/2)+cos2A`的值; (2)若`a=sqrt(3)`,求`bc`的最大值.
|
|
|
方法感悟 1.本节公式较多,要对公式的来龙去脉了解清楚,把握住公式的结构,这样才能准确地应用公式,同时注意公式的正用逆用、变形应用. 2.转化的思想是实施三角变换的主导思路,变换包括函数名称变换、角的变换、1的变换、幂的升降变换等等. 3.恒等变形前需分析已知式中角的差异,函数名称的差异,寻求联系,实现转化. 4.条件等式的证明.注意认真观察,发现已知条件和求证等式之间的关系,选择适当的途径运用条件,从已知条件出发,以求证式为目标进行代数或三角恒等变形,逐步推出求证式. 常用的三角变换: (1)角的变换:主要是将三角函数中的角恰当变形,以利于应用公式和已知条件. 如`2alpha=(alpha+beta)+(alpha-beta)`,`2beta=(alpha+beta)-(alpha-beta)`,`alpha=(alpha+beta)/2+(alpha-beta)/2`,`beta=(alpha+beta)/2-(alpha-beta)/2`,`alpha=(2alpha)/2=(alpha+beta-beta)`. (2)函数名称变换:主要是切割化弦、弦切互换、正余弦互换、正余切互换. 如:`tanalpha=sinalpha/cosalpha=1/cotalpha=(2tan(alpha/2))/(1-tan^2(alpha/2))=±root()(sec^2alpha-1)`. `sinalpha=tanalpha*cosalpha=1/cscalpha=±root()(1-cos^2alpha)`等。 |