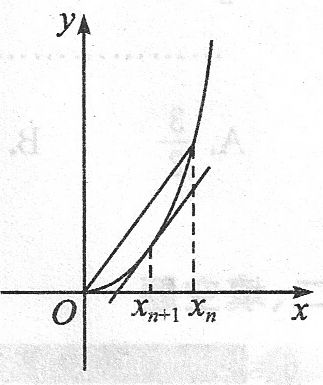考点案例
(在实践中提高能力,在体验中反思感悟,力求独立,力求提高)
1、(2005年高考浙江卷)设点`A_n(x_n,0)`、`P_n(x_n,2^(n-1))`和抛物线`C_n:y=x^2+a_nx+b_n(n∈N^**)`,其中`a_n=-2-4n-1/(2^n-1)`,`x_n`由以下方法得到:`x_1=1`,点`P_2(x_2,2)`在抛物线`C_1:y=x^2+a_1x+b_1`上,点`A_1(x_1,0)`到`P_2`的距离是`A_1`到`C_1`上点的最短距离,…,点`P_(n+1)(x_(n+1),,2^n)`在抛物线`C_n:y=x^2+a_nx+b_n`,点`A_n(x_n,O)`到`P_(n+1)`的距离是`A_n`到`C_n`上点的最短距离.
(1)求`x_2`及`C_1`的方程;
(2)证明`{x_n}`是等差数列.
|
提示 |
示范 |
|
|
分别求出. |
解:(1)由题意,得`A_1(1,O)`,`C1:y=x^2-7x+b_1`
设点`P(x,y)`是`C_1`上任意一点,
则`|A_1P|=sqrt((x-1)^2+y^2)=sqrt((x-1)^2+(x^2-7x+b_1)^2)`
令`f(x)=(x-1)^2+(x^2-7x+b_1)^2`,
则`f'(x)=2(x-1)+2(x^2-7x+b_1)(2x-7)`.
由题意,得`f'(x_2)=0`,
即`2(x_2-1)+2(x_2^2-7x_2+b_1)(2x_2-7)=0`.
又`P_2(x_2,2)`在`C_1`上,∴`2=x_2^2-7x_2+b_1`,
解得`x_2=3`,`b_1=14`.
故`C_1`的方程为`y=x^2-7x+14`.
(2)证明:设点`P(x,y)`是`C_n`上任意一点,
则`|A_nP|=sqrt((x-x_n)^2+(x^2+a_nx+b_n)^2)`
=`sqrt((x-x_n)^2+y^2)`.
令`g(x)=(x-x_n)^2+(x^2+a_nx+b_n)^2`,
则`g'(x)=2(x-x_n)+2(x^2+a_nx+b_n)(2x+a_n)`,
由题意,得`g'(x_n+1)=O`,
即`2(x_(n+1)-x_n)+2(x_(n+1)^2+a_nx_(n+1)+b_n)(2x_(n+1)+a_n)=0`
又∵`2^n=x_(n+1)^2+a_nx_(n+1)+b_n`,
∴`(x_(n+1)-x_n)+2^n(2x_(n+1)+a_n)=0(n≥1)`.
即`(1+2^(n+1))x_(n+1)-x_n+2^na_n=0`.(*)
下面用数学归纳法证明`x_n=2n-1`.
①当`n=1`时,`x_1=1`,等式成立.
②假设当`n=k`时,等式成立,即`x_k=2k-1`.
则当`n=k+1`时,
由(*)知`(1+2^(k+1))x_(k+1)-x_k+2^ka_k=0`.
又`a_k=-2-4k-1/(2^(k-1))`,
∴`x_(k+1)=(x_k-2^ka_k)/(1+2^(k+1))=2k+1`.
即当`n=k+1`时,等式成立.
由①②知,等式对`n∈N^**`成立,∴`{x_n}`是等差数列.
评注:本题主要考查二次函数的求导、导数的应用、等差数列、数学归纳法等基础知识,以及综合运用所学知识分析和解决问颗的能力. |
2、(2005年高考山东卷)已知数列`{a_n}`的首项`a_1=5`,前`n`项和为`S_n`,且`S_(n+1)=2S_n+n+5(n∈N^**)`.
(1)证明数列`{a_n+1}`是等比数列;
(2)令`f(x)=a_1x+a_2x^2+…+a_nx^n`,求函数`f(x)`在点`x=1`处的导数`f'(x)`,并比较`2f'(1)`与`23n^2-13n`的大小
.
|
提示 |
示范 |
|
|
将题中. |
解:(1)证明:由已知`S_(n+1)=2S_n+n+5`,
∴`n≥2`时,`S_n=2S_(n-1)+n+4`,两式相减,得
`S_(n+1)-S_n=2(S_n-S_(n-1))+1`,
即`a_(n+1)=2a_n+1`,从而`a_(n+1)+1=2(a_n+1)`.
当`n=1`时,`S_2=2S_1+1+5`,∴`a_1+a_2=2a_1+6`,
又`a_1=5`,∴`a_2=11`.
从而`a_2+1=2(a_1+1)`.
故总有`a_(n+1)+1=2(a_n+1),n∈N^**`.
又∵`a_1=1`,∴`a_n+1≠0`.
从而`(a_(n+1)+1)/(a_n+1)=2`,即`{a_n+1}`是以`a_1+1=6`为首项,2为公
比的等比数列.
(2)由(1)知`a_n=3×2^n-1`.
∵`f(x)=a_1x+a_2x^2+…+a_nx^n`,
∴`f'(x)=a_1+2a_2x+…+na_nx^(n-1)` .
从而`f'(1)=a_1+2a_2+…+na_n`
=`(3×2-1)+2(3×2^2-1)+…+n(3×2^n-1)`
=`3(2+2×2^2+…+n×2^n)-(1+2+…+n)`
=`3[n×2^(n+1)-(2+2^2+…+2^n)]-(n(n+1))/2`
=`3[n×2^(n+1)-2^(n+1)+2]-(n(n+1))/2`.
=`3(n-1)*2^(n+1)-(n(n+1))/2+6`
由上`2f'(1)-(23n^2-13n)`
=`12(n-1)*2^n-12(2n^2-n-1)`
=`12(n-1)*2^n-12(n-1)(2n+1)`
=`12(n-1)[2^n-(2n+1)]`. (*)
当`n=1`时,(*)式=O,∴`2f'(1)=(23n^2-13n)`;
当`n=2`时,(*)式=-12<0,
∴`2f'(1)<(23n^2-13n)`;
当`n≥3`时,`n-1>0`,
又`2^n=(n+1)^2=C_n^0+C_n^1+…+C_n^(n-1)+C_n^n≥2n+2>2n+1`。
∴`(n一1)[2^n一(2n+1)]>0`,即(*)式>0,
从而`2f'(1)>(23n^2-13n)`.
评注:
数列与函数、方程、不等式的综合性试题是近几年高考的热点题型,解题时要注意沟通数列与函数的内在联系,灵活运用函数的思想方法求解,在该类问题的求解过程中往往会遇到递推数列,因此掌握递推数列的常见解法有助于该类问题的解决,其中所涉及的不等式问题通常可采用放缩法、比较法或归纳
猜想一证明的数学归纳法解决.. |
3、(2006湖北高考文20)设数列`{a_n}`的前`n`项和为`S_n`,点`(n,S_n/n)(n∈N^**)`均在函数`y=3z-2`的图象上.
(1)求数列`{a_n}`的通项公式;
(2)设`b_n=3/(a_na_(n+1))`是数列`{b_n}`的前`n`项和,求使得`T_n<m/20`对所有`n∈N^**`都成立的最小正整数`m`.
|
提示 |
示范 |
|
|
`C_U. |
解:(1)依题意得`S_n/n=3n-2`,即`S_n=3n^2-n`.
当`n≥2`时,`a_n=S_n-S_(n-1)=(3n^2-2n)-[3(n-1)^2-2(n-1)]=6n-5`;
当`n=1`时,以`a_1=S_1=3×1^2-2×1=1=6×1-5`.
所以`a_n=6n-5(n∈N^**)`.
(2)由(1)得`b_n=3/(a_na_(n+1))=3/((6n-5)[6(n+1)-5])=1/2(1/(6n-5)-1/(6n+1))`,
故`T_n=sum_(i=1)^oob_i=1/2[(1-1/7)+(1/7-1/13)+…+(1/(6n-5)-1/(6n+1))]=1/2(1-1/(6n+1))`.
因此,使得`1/2(1-1/(6n+1))<m/20(n∈N^**)`成立的`m`必须
且仅需满足专≤斋,即m≤]0,故满足要求的最小整数`m`为]O.
评注:本小题主要考查等差数列、数列求和、不等式等基础知识和基本运算技能,考查分析问题的能力和推理能力.
|
4、(2005上海高考理20)假设某市2004年新建住房400万平方米,其中有250万平方米是低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%,另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米,那么,到哪一年底
(1)该市历年所建中低价房的累计面积(以2004年为累计的第一年)将首次不少于4750万平方米?
(2)当年建造的低价房的面积占该年建造住房面积的比例首次大于85%?
|
提示 |
示范 |
|
|
集合中的. |
解:(1)设中低价房面积形成数列`{a_n}`,由题意可知`{a_n}`是等差数列.其中`a_1=250,d=50`.
则`S_n=250n+(n(n-1))/2×50=25n^2+225n`,
令`25n^2+225n≥4750`,
即`n^2+9n-190≥O`,而`n`是正整数,∴`n≥10`.
∴到2013年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米.
(2)设新建住房面积形成数列`{b_n}`,由题意可知`{b_n}`是等比数列.其中`b_1=400,q=1.08`.
则`b_n=400(1.08)`.
由题意可知`a_n>0.85b_n`.
有`250+(n-1)•50>400•(1.08)^(n-1)•0.85`.
用计算器解得满足上述不等式的最小正整数`n=6`.
∴到2009年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.
评注:
本题主要考查学生运用所学数列知识解决实际问题的能力,以及数学建模能力. |
5、(2006上海高考理21)已知有穷数列`{a_n}`共有`2k`是项`(整数k≥2)`,首项`a_1=2`,设该数列的前`n`项和为`S_n`,且`a_(n+1)=(a-1)S_n+2(n=1,2…,2k-1)`,其中常数`a>1`.
(1)求证:数列`{a_n}`是等比数列;
(2)若`a=2^(2/(2k-1))`,数列`{b_n}`满足`b_n=1/nlog_2(a_1a_2…a_n)(n=1,2,…,2k)`,求数列`{b_n}`的通项公式;
(3)若(2)中的数列`{b_n}`满足不等式
`|b_1-3/2|+|b_2-3/2|+…+|b_(2k-1)-3/2|+|b_(2k)-3/2|≤4`,求`k`的值.
|
提示 |
示范 |
|
|
(提示内容) |
解:(1)`a_(n+1)=(a-1)S_n+2`,
①
当`n≥2`时,`a_n=(a-1)S_(n-1)+2`, ②
两式相减得
`a_(n+1)-a_n=(a-1)(S_n-S_(n-1))=(a-1)a_n`,
∴`a_(n+1)=aa_n`,
∴`a_(n+1)/a_n=a`为常数.
∴数列`{a_n}`是以`a_1=2`为首项,以`a`为公比的等比数列.
(2)由(1)知`a_n=2*a^(n-1)`,
∴`b_n=1/nlog_2(2*2a*2a^2*…*2a^(n-1))`
=`1/nlog_2(2^n*a^(1+2+…+(n-1)))`
=`1/n(n+log_2(a^(n(n-1))/2))=1+1/n*(n(n-1))/2*log_2a=1+(n-1)/2*2/(2k-1)=1+(n-1)/(2k-1)`.
(3)`|b_n-3/2|=|(n-1)/(2k-1)-1/2|=|(2n-2k-1)/(2()2k-1)|`
∴=`|b_1-3/2|+|b_2-3/2|+…+|b_(2k-1)-3/2|+|b_(2k)-3/2|`
=`|(1-2k)/(2(2k-1))|+|(3-2k)/(2(2k-1))|+…+|(2k-3)/(2(2k-1))|+|(2k-1)/(2(2k-1))|`
=`2[1/(2(2k-1))+3/(2(2k-1))+…+(2k-3)/(2(2k-1))+(2k-1)/(2(2k-1))]`
=`(1+3+5+…+(2k-1))/(2k-1)=k^2/(2k-1)`.
令`k^2/(2k-1)≤4`,即`k^2-8k+4≤0`,
∴`4-2sqrt(3)≤k≤4-2sqrt(3)`.
又∵`k≥2,k∈Z`,
∴`k`的值为2,3,4,5,6,7.
评注:本题主要考查数列知识的综合运用以及对数知识和解绝对值不等式的能力. |
|