|
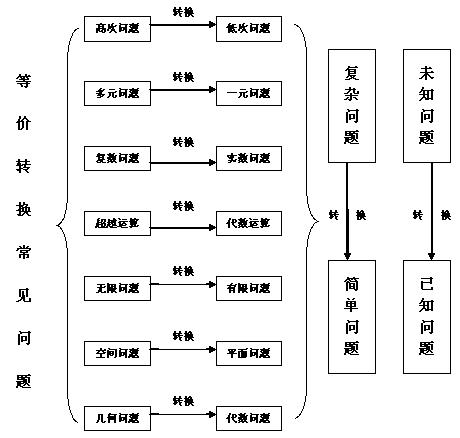
网络结构
|
|
要点归纳 一、什么是化归与转达化思想 所谓化归思想方法,就是在研究和解决有关数学问题时采用某种手段将问题通过变换使之转化,进而达到解决的一种方法,一般总是将复杂的 问题通过变换转化为简单的问题,将难解的问题通过变换转化为容易求解的问题,将未解决的问题变换转化为已解决的问题。 化归思想方法的主要特点是它的灵活性和多样性,一个数学问题,我们可以视其为一个数学系统或数学结构,组成其要素之间的相互依存和相互联系的形式是可变的,其形式并非唯一,而是多种多样,所以,应用数学变换的方法去解决有关数学问题时,就没有统一的模式要遵循,在此正需要我们依据问题本身提供的信息,处用所谓的动态思维,去寻求有利于问题解决的变换途径和方法,并从中进行一番选择。 二、运用化归与转化思想解题策略 1.转化包括等价和非等价转化 等价转化要求在转化过程中的前因与后果既是充分的,又是必要的,这样的转化能保证转化的结果仍为原问题所需要结果;不等价转化的过程仅是充分的或仅是必要的,它不能保证转化后的结果就是原问题所需要的结果,还需要其他辅助手段帮助我们得到准确的结果,既使是这样,非等价转化也能给我们带来思维的启迪,找到解决问题的突破口,是破解难点的重要思维方法之一。 2.转化与化归的原则 将不熟悉的和较难的问题化为熟知的易解的或已经解决的问题;将抽象的问题转化为具体的直观的问题;将复杂的问题转化为简单的问题;将一般性的问题转化为直观的特殊的问题;将实际问题转化为数学问题,使问题便于解决。 3.转化与化归的基本类型 (1)正与反、一般与特殊的转化,即正难则反,特殊化原则。 (2)常量与变量的转化,即在处理多元问题时,选取其中的常量(或参数)当“主元”,其他的变量看作常量。 (3)数与形的转化,即利用对数量关系的讨论来研究图形性质,也可利用图形直观提供思路,直接地反映函数或方程中的变量之间的关系。 (4)数学各分支之间的转化,如利用向量方法解立体几何问题,用解析几何方法处理平面几何、代数、三角问题等。 (5)相等与不等之间的转化,如利用均值不等式、判别式等。 (6)实际问题与数学模型的转化。 4.常见的转化方法 转化与化归思想用在研究、解决数学问题时思维受阻或寻求简单方法,从一种状况转化为另一种情形,也就是转化到另一种情境,使问题得到解决,这种转化是解决问题的有效策略,同时也是成功的思维方式,那么选择哪些途径可以实现这个转化过程呢?常见的转化方法有: (1)直接转化法:把原问题直接转化为基本定量、基本公式或基本图形问题。 (2)换元法:运用“换元”把超越式转化为有理式或使整式降幂等,把较复杂的函数、方程、不等式问题转化为易于解决的基本问题。 (3)数形结合法:研究原问题中数量关系(解析式)与空间形式(图形)关系,通过互相变换,获得转化途径。 (4)参数法:引进参数,使原问题的变换具有灵活性,易于转化。 (5)构造法:“构造”一个合适的数学模型,把问题变为易于解决的问题。 (6)坐标法:以坐标系为工具,用计算方法解决几何问题,是转化方法的一个重要途径。 (7)类比法:运用类比推理,猜测问题的结论,确定转化途径。 (8)特殊化方法:把原问题的形式向特殊化形式转化,并证明特殊化后的结论适合原问题, (9)一般化方法:若原问题是某个一般化形式问题的特殊形式且又较难解决,可将问题通过一般化的途径进行转化。 (10)等价问题法:把原问题转化为一个易于解决的等价命题,达到转化目的。 (11)加强命题法:在证明不等式时,原命题难以得证,往往把命题的结论加强,即把命题的结论加强为原命题的充分条件,反而能将原命题转化为一个较易证明的命题(加强命题法是非等价转化方法)。 (12)补集法:如果正面解决原问题有困难,可把原问题的结果作集合A,而把包含该问题的整体问题的结果类比为全集U,通过解决全集U及补集`C_UA`使原问题获得解决。 |
| 典型案例 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高)
1、对于函数`y=f(x)(x inD)`,存在`x_0 inD`满足`f(x_0)=x_0`,则称`x_0`为函数`f(x)`的不动点,若函数`f(x)=x/(a(x+2))`有唯一不动点,且`x_1=1000`,`1/x_(n+1)=f(1/x_0)`,`n inN^*`,则`x_2007`的值为(
)
2、设`f(x)=4^x/(4^x+2),`求`f(1/2003)+f(2/2003)+…+f(2002/2003)`的值。
3、已知数列`{a_n}`中,`a_1=1,a_n=(2S_n^2)/(2S_n-1)(n>=2),`求通项`a_n`及前`n`项和`S_n`。
|
|
|
思想感悟 1、用集合的概念解题; [缺] |