专题一函数与方程思想

网络结构

要点归纳

典型案例

应用训练

思想感悟

网络结构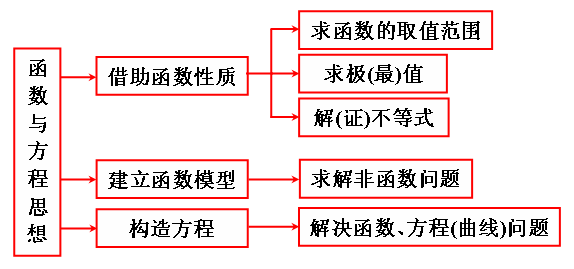

    要点归纳
    一、什么是函数与方程思想?
    1、函数思想是用运动和变化的观点，集合与对应的思想，即用函数的观点去分析和研究数学问题中的数量关系，建立函数关系或构造函数，运用函数的图象和性质去分析问题、转化问题，从而使问题获得解决，是对函数概念的本质认识．
    2、方程思想是分析数学问题中变量间的等量关系，建立方程或方程组，或者构造方程，通过解方程或方程组或者运用方程的性质去分析、转化问题，使问题获得解决，是对方程概念的本质认识．
    二、运用函数与方程思想解题策略
    1、函数思想
    (1)引入变量，确定函数关系
    在数学各分支中若遇到有关不等式、方程及最值之类的问题，利用函数观点加以分析，常可使问题变得明了，从而易于找到一种适当的解题途径．
    (2)选定主元，揭示函数关系
    如何从一个含有多个变元的数学问题里，选定合适的主变元，从而揭示其中主要的函数关系，有时便成了数学问题能否“明朗化”的关键所在．
    (3)选取变元，构造函数关系
    选取变元，构造函数关系来解决数学问题，这是运用函数思想解题的较高层次，只有平时多加训练并注意积累，才能运用自如．
    (4)解答实际问题，关键在于建立目标函数
    对于实际应用题，首先要读懂文字说明，再将其翻译成数学语言，建立数学模型和函数关系式，利用函数的性质、重要不等式或有关知识进行解答．
    (5)将数列看作自变量为n的函数
    等差、等比数列通项公式，前n项和公式都可看成n的函数，因此，某些等差(比)数列问题常可用函数思想来分析或用函数方法来解决．
    2、方程思想
    (1)选定待定系数，建立方程
    待定系数法的实质就是方程思想，它把待定的未知数与已知数等同看待来建立等式，即得到方程(组)．
    (2)利用根与系数的关系或根的判别式构造方程
    如果题设条件中具备或经过变形整理后具备`x_1+x_2=a，x_1•x_2=b`的形式，则可以利用根与系数的关系；具备`b^2－4ac`≥0或`b^2－4ac`≤0的形式，可利用根的判别式构造一元二次方程．
    (3)利用变量代换构造方程
    对某些问题，巧妙地进行变量代换，经适当整理后可使问题转化为关于某变数的方程形式，可应用方程思想来解题．
    三、注意事项
    1、函数思想与方程思想是密切相关的
    对于函数y=f(x)，当y=0时，就转化为方程f(x)=0，也可以把函数式y=f(x)看作二元方程y－f(x)=0；反之，方程问题也可以转化为函数问题加以解决，如解方程f(x)=0，就是求函数y=f(x)的零点．
    2、函数与不等式也可相互转化
对于函数y=f(x)，当y>O时就化为不等式f(x)>0，借助于函数图象与性质可解决相关问题，而研究函数性质，也离不开解不等式．
    3、在许多数学问题中，一般都含有多元参变量，根据题目需要，变换“主元”往往能出奇制胜，但不要脱离题目本身的条件．
    4、函数与方程思想与其他几种思想方法相互融合使用，才能显示出其强大威力．不要脱离其他思想方法单独“钻题”，浪费时间．

　

    典型案例
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)
    1、已知数列`{a_n}`是等差数列，若`S_n=10，S_(2n)=50，求S_(3n).

提示	示范
分别求出.
解:由条件知数列`{S_n/n}`是等差数列，故`(n，S_n/n)，(2n，(S_(2n))/(2n))， (3n，(S_(3n))/(3n))`三点共线，所以`(50/(2n)－10/n)/(2n－n)=(S_(3n)/(3n)－10/n)/(3n－n)`．解得`S_(3n)=120`．评注:本题的解法比较多，但构造相应的函数再解决问题显然简单快捷．由`{a_n}`是等差数列可得`S_n/n=(a_1+a_n)/2`，从而`{S_n/n}`也是等差数列.

2、设n是大于1的自然数，证明`(1+1/3)(1+1/5)…(1+1/(2n－1))>sqrt(2n+1)/2`．

提示	示范
将题中.
解:证明方法较多，而应用函数的单调性来证，过程简捷明了．设`f(n)=(1+1/3)(1+1/5)…(1+1/(2n－1))2/sqrt(2n+1)` (n≥2)，则`f(n－1)/f(n)=(1+1/(2n－1))•(2/sqrt(2n+3))/(2/sqrt(2n+1))=sqrt((4n^2+8n+4)/(4n^2+8n+3))>1` ∴f(n)是单调递增函数． ∵`f(2)=4/3•2/sqrt(5)=sqrt(64/45)>1`，故f(n)>1，即`(1+1/3)(1+1/5)…(1+1/(2n－1))>sqrt(2n+1)/2` 评注: 应用函数的性质证明不等式，关键在于构造一个适当的函数，且能较方便地判断该函数的有关性质．

    3、已知函数f(x)=x－sinx，数列`{a_n}`满足：0<`a_1`<1，`a_(n+1)=f(a_n)`，n=1，2，3，…．
    求证：(1)`0<a_(n+1)<a_n<1`；
    (2)`a_(n+1)<1/6a_n^3`．

提示	示范
`C_U.
解:`(1)先用数学归纳法证明0<`a_n`<1，n=1，2，3，…． (i)当n=l时，由已知，结论成立． (ii)假设当n=k时结论成立，即0<`a_k`<1．因为当O<x<l时，f'(x)=1－cosx>0，所以f(x)在(0，1)上是增函数．又f(x)在[0，1]上连续，所以f(0)<f(`a_k`)<f(1)，即0<`a_(k+1)`<1－sin1<1．故当n=k+1时，结论成立．由(i)(ii)，可知0<`a_n`<l对一切正整数都成立．又因为0<`a_n`<1时，`a_(n+1)－a_n=a_n－sin a_n－a_n=－sin a_n<0`，所以`a_(n+1)<a_n`．综上所述`0<a_(n+1)<a_n<1`． (2)设函数`g(x)=sin x－x+1/6x^3，0<x<1`．由(1)，知当0<x<1时，sinx<x．从而`g'(x)=cosx－1+x^2/2=－2sin^2 x/2+x^2/2>－2(x/2)^2+x^2/2=0`．所以g(x)在(0，1)上是增函数．又g(x)在[O，1]上连续，且g(0)=0，所以当0<x<1时，g(x)>0成立．于是g(a_n)>0，即`sin a_n－a_n+1/6a_n^3>0`．故`a_(n+1)<1/6a_n^3`．评注:数列就是一类特殊的函数，利用函数的单调性来研究数列问题，这是历年高考的热点问题．

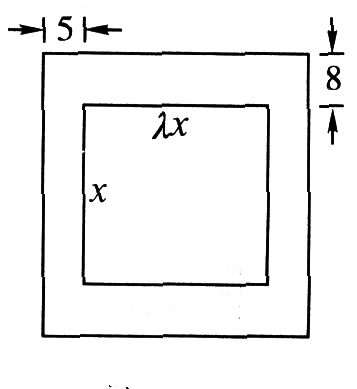
4、设计一幅宣传画，要求画面面积为4840 `cm^2`，画面的宽与高的比为λ(λ<1)，画面的上、下各留8cm的空白，左、右各留5 cm的空白．怎样确定画面的高与宽的尺寸会使宣传画所用纸张面积最小?

提示	示范
解答实际问题，关键在于建立目标函数，同时确定其定义域.
解:设画面高为x cm，则宽为λx cm，且λ`x^2`=4840，又设纸张面积为y．如图所示，则有 `y=(x+16)(λx+10)=λx^2+16λx+10x+160=4840+160+16x•4840/x^2+10x=5000+(16×4840)/x+10x`．由`lambda=4840/x^2`<1，得函数的定义域为`(22sqrt(10)，+∞)`． ∵`(16×4840)/x+10x`≥`2 sqrt(16×48400)`，当且仅当`(16×4840)/x=10x`，即x=88时，取等号，而x=88>`22sqrt(10)`，高x=88时，y有最小值，此时宽为4840÷88=55(符合宽与高的比λ<1)．答：画面高为88 cm，宽为55 cm时，所用纸张面积最小．评注:运用函数的思想方法，先把所用纸张的面积y表示成画面的高x的函数，写出定义域，再求函数的最小值及相应的宽与高．

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。