一、高考大纲
考试内容:
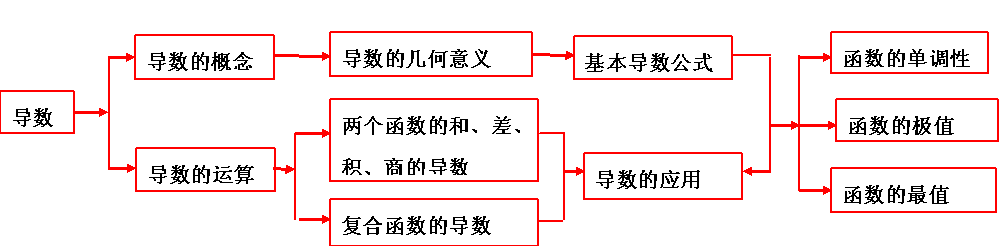
导数的概念。导数的几何意义。几种常见函数的导数。
两个函数的和、差、积、商和导数。复习函数的导数。基本导数公式。
利用导数研究函数的单调性和极值。函数的最大值和最小值。
考试要求:
(1)了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等);掌握函数在一点处的导数的定义和导数的几何意义;理解导函数的概念。
(2)熟记基本导数公式(c,xm(m为有理数),sinx,cosx,ex,ax,lnx, logax
的导数);掌握两个函数和、差、积、商的求导法则。了解复合函数的求导法则,会求某些简单函数的导数。
(3)理解可导函数的单调性与其导数的关系;了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值。
二、高考要览
| 考试内容 |
能力层次 |
高考要求 |
考题年份分值 |
| 导数 |
了解 |
导数概念;复合函数求导法则 |
|
2004 |
2005 |
2006 |
2007 |
2008 |
| 全国I.5 |
|
|
|
|
| 全国Ⅳ.5 |
|
|
|
|
| 湖北.5 |
湖北.5 |
|
|
|
| 浙江.5 |
|
|
|
|
| 湖南.4 |
湖南.5 |
湖南13.4 |
|
|
| 重庆.4 |
重庆.4 |
|
|
|
| |
江西.5 |
|
|
|
| |
北京.4 |
北京16.13 |
|
|
| |
江苏.4 |
|
|
|
| |
|
安徽7.5 |
|
|
| |
|
安徽20.12 |
|
|
| |
|
辽宁22.12 |
|
|
|
| 理解 |
导函数概念 |
| 掌握 |
函数在一点处的导数的定义和导数的几何意义;基本导数公式;和、差、积、商的求导法则;会求简单函数的导数 |
|
导数应用 |
了解 |
可导函数的单调性与其导数的关系;可导函数在某点取得极值的必要和充分条件 |
| 2004 |
2005 |
2006 |
2007 |
2008 |
| 全国I.4 |
|
全国I21.14 |
|
|
| 全国Ⅱ.12 |
全国Ⅱ.12 |
|
|
|
| 全国Ⅱ.12 |
|
|
|
|
| |
全国Ⅲ.12 |
|
|
|
| 江苏.5 |
江苏.12 |
|
|
|
| 湖北.5 |
湖北.12 |
|
|
|
| 湖北.12 |
|
|
|
|
| 福建.5 |
福建.12 |
|
|
|
| 福建.12 |
|
|
|
|
| 天津.14 |
|
|
|
|
| 广东.12 |
广东.5 |
|
|
|
| 广东.12 |
|
|
|
|
| 湖南.5 |
|
|
|
|
| 湖南.12 |
|
|
|
|
| 浙江.12 |
|
|
|
|
| 重庆.12 |
重庆.12 |
|
|
|
| 辽宁.12 |
辽宁.12 |
|
|
|
| 安徽春.12 |
|
|
|
|
| |
江西.12 |
江西5.5 |
|
|
| |
|
江西17.5 |
|
|
| |
山东.12 |
|
|
|
| |
|
天津9.5 |
|
|
| |
|
天津20.12 |
|
|
|
| 掌握 |
会求一些实际问题的最大值和最小值 |
三、命题趋势
从上表可以看出近几年本章考查呈现以下特点:
1、题型和题量:一般为一个小题和一个大题,小题主要考查导数的概念、四则运算及简单的应用,大题主要考查单调性、极值、最值问题及应用问题.
2、知识点考查:考查的重点为用导数求函数的单调区间、极值、最值或已知函数的单调区间、极值、最值求参数的取值范围或参数的值.
3、难度与创新:导数是近几年的教材中增加的内容,高考对这部分内容越考越难,出题的形式多种多样,大题逐步由中档题向综合题过渡.
四、复习建议
根据本章知识的重要性以及高考对本章内容的考查情况,复习时应注意以下几点:
1、导数是中学内容中较为重要的知识.由于其应用的广泛性,为我们解决所学过的有关函数问题提供了一般性的方法,运用它可以简捷地解决一些实际问题.本章中导数的概念、求导运算、函数的单调性、极值和最值是重点知识
.因此,要掌握其概念,会求函数的导数,会用求导的方法判断或论证函数的单调性,会求函数的极值和最值,会用导数解决一些实际问题.
2、要从实际背景出发了解导数的定义,及简单函数导函数的求法(用定义)并注意函数值的改变量要与自变量的改变量对应.
3、通过适量运算,掌握简单函数导数的求法,并熟记常见函数的导数公式及求导法则.
4、导数在研究函数的单调性、求函数最值两方面的应用是本章重点,尤其在解应用题时的作用更应引起重视.
五、思想与方法综览
1、函数与方程思想
函数思想是指用联系变化的观点分析问题,通过函数的形式把问题中的数量关系表示出来,运用函数的概
念、图象、性质、求导等对问题加以研究,使问题获得解决.函数与方程二者密切不可分,如函数的解析式`y=f(x)` 也可看成方程.函数与方程思想体现了动与静、
变量与常量的辩证统一,是重要的数学方法之一.
例1(2006年北京)已知函数`f(x)=ax^3+bx^2+cx`在点`x_0`处取得极大值5,其导函数`y=f′(x)`的图象经过点(1,0),(2,0),如图所示
.求:
(1)`x_0`的值;
(2)`a,b,c`的值.
解答:解法一:(1)由图象可知,在`(-00,1)上,f′(x)>0`
故`f(x)`在`(-oo,1),(2,+oo)`上递增,在`(1,2)`上递减.因此`f(x)`在`x=1`处取得极大值,所以`x_0=1`
(2)`f′(x)=3ax^2+2bx+c,由f′(1)=0.
f′(2)=0,f(1)=5,得{(3a+2b+c=0),(12a+4b+c=0),(a+b+c=5):}`
解得`a=2,b=-9,c=12`
解法二:(1)同解法一
(2)设`f′(x)=m(x-1)(x-2)=mx^2-3mx+2m`,又` f′(x)=3ax^2+2bx+c`
所以`a=m/3,b=-3m/2,c=2m,f(x)=(m/3)x^3-3/2mx^2+2mx`
`由f(1)=5,即m/3-3/2m+2m=5,得m=6,所以a=2,b=-9,c=12`.
2、化归与转化思想
化归与转化是指在处理问题时,把待解决或难解决的问题,通过某种转化过程,化归为一类已经解决的或比较容易解决的问题,从而求得原问题的解.化归与转化思想在数学中非常广泛,如未知向已知的转化,
新知识向旧知识的转化,复杂问题向简单问题的转化,实际问题向数学问题的转化等.
例2 已知一列椭圆`C_n:x^2+y^2/b_n^2=1,0<b_n<1,n=1,2,…`,若椭圆`C_n`上有一点`P_n`,使`P_n`到右准线`l_n`的距离`d_n`是`|P_nF_n|与|P_nG_n|`的等差中项,其中`F_n、G_n`,分别是`C_n`的左右
焦点.
(1)试证:`b_n<=sqrt(3)/2(n>=1)`;
(2)取`b_n=sqrt(2n+3)/(n+2)`,并用`S_n`表示`DeltaP_nF_nG_n`的面积,试证:`S_1<S_2且S_n>S_
(n+1)(n>=3)`
解答:(1)由题设及椭圆的几何性质有`2d_n=|P_nF_n|+|P_nG_n|=2,故d_n=1`
设`c_n=sqrt(1-b_n^2),则右准线方程为l_n:x=1/c_n`
因此,由题意`d_n=1`应满足`1/c_n-1<=d_n<=1/c_n+1`,
即`{(1/c_n-1<=1),(0<c_n<1):}`解得`1/2<=c_n<1`,即`1/2<=sqrt(1-b_n^2)<1`
从而对任意`n>=1,b_n<=sqrt(3)/2`
(2)设点`P_n`的坐标为`(x_n,y_n)`,则由`d_n=1`及椭圆方程易知`x_n=1/c_n-1`
`y_n^2=b_n^2(1-x_n^2)=(1-c_n^2)[1-(1/c_n-1)^2]=1/c_n^2(-2c_n^3+c_n^2+2c_n-1)`.
因为`|F_nG_n|=2c_n`,故`DeltaP_nF_nG_n`的面积为`S_n=c_n|y_n|`,从而`S_n^2=-2c_n^3+c_n^2+2c_n-1(1/2<=c_n<1)`
令`f(c)=-2c^3+c^2+2c-1`,由`f′(c)=-6c^2+2c+2=0`,得两根`(1+-sqrt(13))/6`,
从而易知`f(c)`在`[1/2,(1+sqrt(13))/6)`内是增函数,而在`((1+sqrt(13))/6,1)`内是减函数.
现在由题设取`b_n=sqrt(2n+3)/(n+2)`,则`c_n=sqrt(1-b_n^2)=(n+1)/(n+2)=1-1/(n+2),c_n`是增数列
.
又易知`c_2=3/4<(1+sqrt(13))/6<4/5=c_3`,故由前已证知`S_1<S_2`,且`S_n>S_n+1(n>=3)`
3、分类讨论思想
分类讨论是重要的数学思想方法之一,它把受多种条件交叉制约、形成错综复杂的问题划分成若干个局部问题,在每一局部问题中,原先的“不确定因素”不再影响问题的解决,当这些局部问题都解决完时,整
个问题也就解决了,分类讨论问题涉及面广、综合性强,在高考题中,从未间断对这一思想的考查.
例3 已知函数`f(x)=-x^2+8x,g(x)=6lnx+m`
(1)求`f(x)`在区间`[t,t+1]`上的最大值`h(t)`;
(2)是否存在实数m,使得`y=f(x)`的图象与`y=g(x)`的图象有且只有三个不同的交点?若存在,求出m的取值
范围;若不存在,说明理由.
解答:(1)`f(x)=-x^2+8x=-(x-4)^2+16`
当`t+1<4, 即t<3时,f(x)在[t,t+1]`上单调递增.`h(t)=f(t+1)=-(t+1)^2+8(t+1)=-t^2+6t+7`
当`t<=4<=t+1时,即3<=t<=4时,h(t)=f(4)=16`
当`t>4时,f(x)在[t,t+1]上单调递减,h(t)=f(t)=-t^2+8t`
综上,`h(t)={(-t^2+6t+7,(t<3)),(16,(3<=t<=4)),(-t^2+8t,t>4):}
(2)函数`y=f(x)的图象与y=g(x)`的图象有且只有三个不同的交点,即函数`varphi(x)=g(x)-f(x)`的图象与x轴的正半轴有且只有三个不同的交点,所以`varphi(x)=x^2-8x+6lnx+m, varphi′(x)=2x-8+6/x=(2x^2-8x+6)/x=(2(x-1)(x-3))/x(x>0)`
当`x in (0,1)时,varphi′(x)>0, varphi(x)`是增函数;
当`x in (1,3)时,varphi′(x)<0, varphi(x)`是减函数;
当`x in (3,+00)时,varphi′(x)>0,varphi(x)`是增函数;
当`x=1或x=3时,varphi′(x)=0`
所以` varphi(x)的极大值= varphi(1)=m-7, varphi(x)的极小值= varphi(3)=m+8ln3-15`
因为当x充分接近0时,` varphi(x)<0,当x充分大时,varphi(x)>0`所以要使`arphi(x)`的图象与x轴正半轴有三个不同的交点,必须且只须`{( varphi(x)的极大值=m-7>0),(varphi(x)的极小值=m+6ln3-15<0):},即7<m<15-6ln3`所以存在实数`x`,使得函数`y=f(x)与y=g(x)`的图象有且只有三个不同的交点,m的取值范围为`(7,15-6ln3)`
4、构造思想
“构造”是一种重要而灵活的思维方法.应用好构造思想解题的关键是:一要有明确的方向.即为什么目
的而构造,二是要弄清条件的本质特点,以便重新进行逻辑组合.
例4 已知`a、b`为实数,且`b>a>e`,其中`e`为自然对数的底,求证`a^b>b^a`
分析:通过考察函数的单调性证明不等式也是常用的一种方法.
解答:`.:b>a>e,:.要证a^b>b^a,只要证blna>alnb`
`.:b>a>e,:.lna>1且a/b<1,:.f′(b)>0`
`:.`函数`f(b)=b•lna-alnb`在`(e,+00)`上是增函数.
`:.f(b)>f(a)即blna-alnb>alna-alna=0即blna-alnb>0,:.blna>alnb,a^b>b^a`.
|