第九章  直线、平面、简单几何体(B)
 §9.6 空间距离

复习目标 知识梳理 应用举例 实践体验 拓展探究 基础训练 提高训练 学习感悟

    一、复习目标
    掌握空间两点间距离的公式，掌握点和面、直线和直线、直线和平面、平面和平面距离的概念(对于异面直线的距离，只要求会利用给出的公垂线计算距离或会计算在坐标表示下的距离)，会解决—些简单的距离问题．

    二、重点难点
    (这里输入)

    三、特别提示
    (1)从空间中各种距离的定义看，它们基本上都是转化为两点间的距离来计算．因此，会求空间中两点的距离是基础，求点到直线和点到平面的距离是重点，求异面直线的距离是难点．求解距离问题要注意运用化归与转化思路：面面距离`rarr`线面距离`rarr`点面距离`rarr`点点距离．


    (2)点与点的距离，点到直线的距离，一般用三垂线定理“定性”．


    (3)给出公垂线的两条异面直线的距离，先进行论证(先定性)，然后再计算(后定量)．


    (4)点到平面的距离是有关距离问题的重点，它主要由三种方法求得：

    ①用定义，直接能作出这段距离，经论证再计算；

    ②用二面角的平面角性质：平面角的一边上任意一点到另一边的距离都垂直于第二边所在的平面 ．先作“点”所在平面与“平面”组成的二面角的平面角，过“点”作平面角另一边的垂线，垂线长即为此“点”到“平面”的距离；

    ③转化为锥体的高，用三棱锥体积公式求点到平面的距离．这三种方法中第二种推理和计算量都较大．


    (5)异面直线间距离(除“3”指出的外)、直线与其平行的平面间的距离和两平行平面间的距离都转化为求点到平面间距离计算．

    知识梳理

    1、一点到它在一个平面内的射影的距离叫做这一点到这个平面的距离．

　

    2、一条直线上的任一点到与它平行的平面的距离，叫做这条直线到平面的距离．

　

    3、和两个平行平面同时垂直的直线，叫做这两个平面的公垂线，公垂线夹在平行平面间的部分，叫做这两个平面的公垂线段，公垂线段的长度叫做两个平行平面的距离．

　

    4、和两条异面直线都垂直相交的直线，叫做两条异面直线的公垂线，公垂线夹在异面直线间的部分，叫做两条异面直线的距离，公垂线段的长度叫做两条异面直线的距离．

　

    5、任意两条异面直线有且只有一条公垂线，公垂线段是连结两条异面直线上两点的线段中最短的一条．

　

    6、距离公式    

    已知两条异面直线所成的角为`theta`，如图，在直线`a、b`上分别取`E、F`，已知`A'E=m`，`AF=N`，`EF=l`，则公垂线段`A A'`的长度为`d=sqrt(l^2-m^2-n^2-+2mncostheta)`

　

    应用举例
    一、应用特点
    1、点到直线、点到平面的距离的求法
    2、直线与平面的距离和平面与平面的距离
    3、距离间的相互转化

    二、案例示范
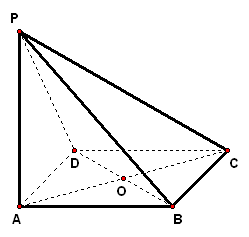
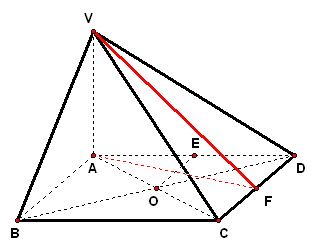
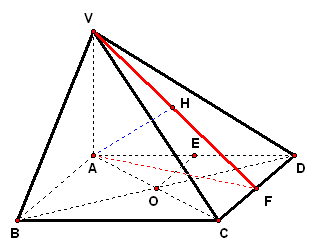
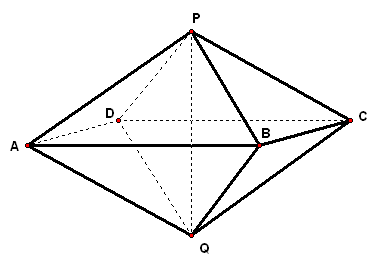
    回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范

    1、如图，`ABCD`是菱形，`PA_|_平面ABCD`，`PA=AD=2`，`/_BAD=60°`

    (1)求证：平面`PBD_|_`平面`PAC`

    (2)求点`A`到平面`PBD`的距离

    (3)求二面角`D-PB-C`的大小

　
    提示 示范 　

   

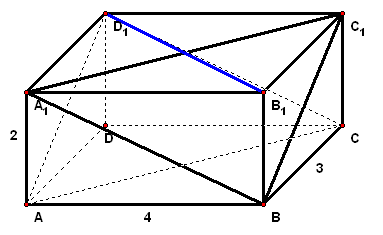
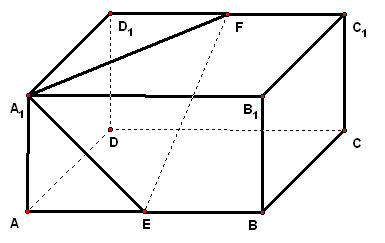
    2、长方体`ABCD-A_1B_1C_1D_1`中，`AB=4`，`BC=3`，`C C_1=2`

    (1)求证：平面`A_1BC_1"//"`平面`ACD`
    (2)求(1)中两个平行平面间的距离
    (3)求点`B_1`到平面`A_1BC_1`的距离
    提示 示范 　

   

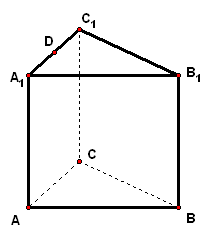
    3、直三棱柱`ABC-A_1B_1C_1`的两底面是等腰直角三角形，且`/_ABC=90°`，在`A_1C_1`上取一点`P`，使`A_1P=m`，`PC_1=``n`，使二面角`P-AB-C`的大小为`alpha`，求`C`点到平面`PAB`的距离

    提示 示范

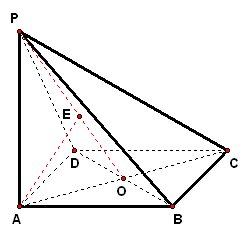
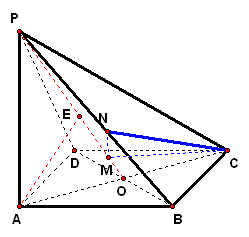
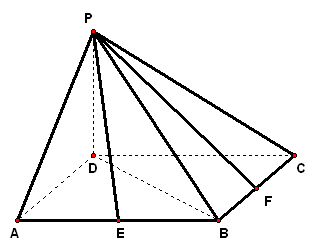
    实践体验
    在实践中提高能力，在体验中反思感悟，力求独立，力求提高

    1、如图，已知正方形`ABCD`，边长为1，过点`D`作`PD_|_平面ABCD`，且`PD=1`，`E`、`F`分别是`AB`和`BC`的中点
    (1)求`D`点到平面`PEF`的距离
    (2)求直线`AC`到平面`PEF`的距离
    提示 示范 　

    

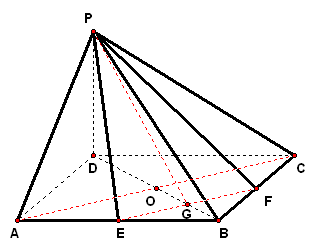
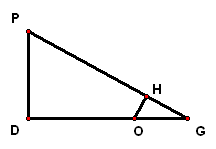
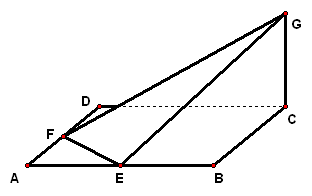
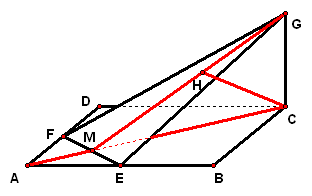
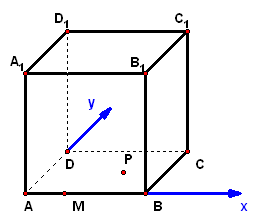
    2、如图，已知正方体`ABCD`的边长为`4`，`E、F`分别是`AB、AD`的中点，`GC=2`且`GC_|_`平面`ABCD`，求`C`点到平面`EFG`的距离

                                                  

    提示 示范 　

    拓展探究
    1、如图，在四棱锥`V-ABCD`中，底面四边形`ABCD`是边长为4的菱形，并且`/_BAD=120°`，`VA=3`，`VA``_|_`底面`ABCD`，`O`是`AC`、`BD`的交点，`OE_|_VC`于`E`，求：     

    (1)点`V`到`CD`的距离
    (2)异面直线`VC`与`BD`的距离
    (3)点`B`到平面`VCD`的距离
    提示 示范 　

　
    基础训练
    参考答案

 
    提高训练
    参考答案

    学习感悟
    1、空间中距离的求法是教材的重要内容，也是历年高考考查的重点，其中以点与点，点到线，点到面的距离为基础，求其它几种距离一般应化归为求这三种距离．

    2、点到直线或平面的距离是空间最常见的．求解的关键是正确作出图形，确定出垂足位置，充分利用图形性质．例如，点到直线的距离，有时要利用两个平面垂直的性质，在其中一个平面内作出两平面交线的垂线得到．

    3、注意各种距离之间的相互转化，可以运用等体积法或“平行移动”的思想方法．

    4、求距离的方法大致有两种
    (1)直接法：步骤是“作、证、述、算”，即先作表示距离的线段(一定要符合作图规则，避免随意性)，再证明它就是所求的距离，并且要有必要的语言叙述，然后再计算，不能忽视第二步的证明，它涉及到很多几何的逻辑推理．

    (2)间接法：包括等体积法和转化法，转化法即不断地转化点面、线面、面面距离的形式，直到求出为止．

返回

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。