|
一、复习目标
二、重点难点 三、特别提示
找一条直线与平面的交角,要过直线上一点向平面作垂线 ,关键是要找到垂足落在何处,才好求出直线与平面的交角.
二面角的平面角的作法是重点.构作二面角的平面角主要有五种方法: ①根据定义; ②利用三垂线定理; ③当二面角由两个等腰三角形构成时,利用底面的两条中线; ④当求正棱锥侧面夹角时利用全等三角形; ⑤在直棱柱中求截面与底面夹角时,用二面角的面积射影定理斗`S_射=S_斜·costheta`,其中`theta`为二面角大小.
①找出或作出有关的平面角; |
|
知识梳理 1、斜线`AO`与它在平面`alpha`的射影`AB`所成的角`theta_1`叫做斜线和平面所成的角(或斜线和平面的夹角).设`AC`是`alpha`内的一条直线,`AO`与`AC`所成的角为`theta`,`AB`与`AC`所成的角为`theta_2`,则`theta_1`、`theta_2`、`theta`的余弦值关系是`costheta=costheta_1·costheta_2`.
2、平面的斜线和平面所成的角,是这条斜线和这个平面内的任一条直线所成角中最小的角;如果直线和平面垂直,那么就说直线和平面所成的角是直角;如果直线和平面平行或在平面内,那么说直线和平面所成的角是`0°`的角.
3、直线和平面所成角的范围为`[0°,90°]`.
4、斜线和所交平面所成的角的范围为`(0°,90°)`.
5、从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,这两个半平面叫做二面角的面.棱为`l`,两个面分别`alpha、beta`的二面角记为`alpha-l-beta`.
6、一个平面垂直于二面角的棱个`l`,且与两个半平面的交线分别是射线`AO`、`OB`,则`/_AOB`叫做二面角`alpha-l-beta`的平面角.二面角的范围是`(0°,180°)`.二面角是直角的二面角叫做直二面角 .相交成直二面角的两个平面,叫做互相垂直的平面. |
|
应用举例
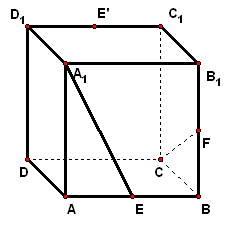
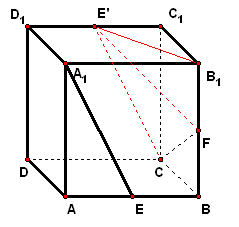
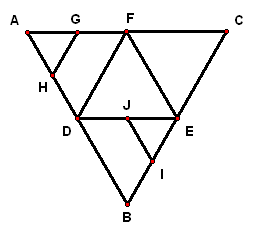
二、案例示范 1、如图,在正方体`ABCD-A_1B_lC_lD_1`中,若`E、F`分别为`AB和BB_1`的中点,求`A_1E`与`CF`所成角的余弦值.
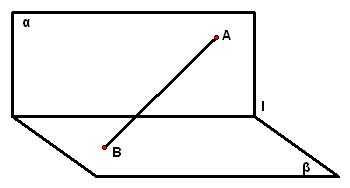
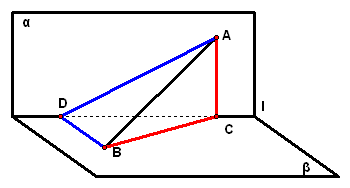
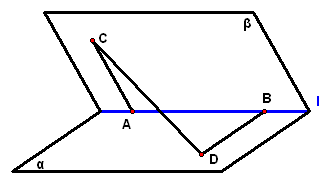
2、在直二面角`alpha-l-beta`内有线段`AB,Ain平面alpha`,`Bin平面beta`,且`AB`与平面`beta`所成的角是`45°`,如果`AB`在平面`beta`内的射影与棱`l`所成角为`45°`,求`AB`与平面`alpha`所成的角
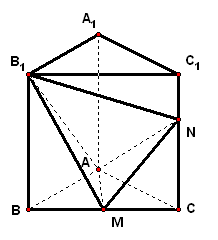
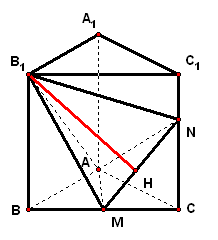
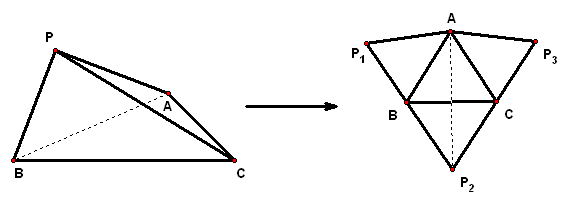
3、如图,已知正三棱柱`ABC-A_1B_1C_1`的侧棱长和底面边长均为`1`,`M`是底面`BC`边上的中点,`N是侧棱C C_1`上的点,且`CN=2C_1N`
|
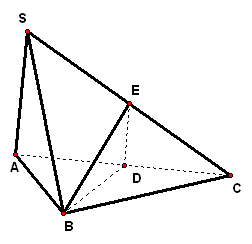
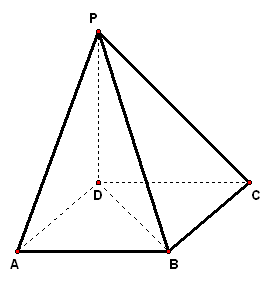
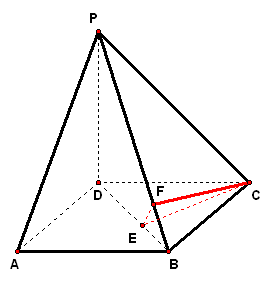
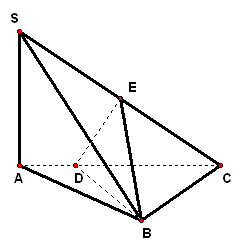
| 实践体验 在实践中提高能力,在体验中反思感悟,力求独立,力求提高 1、在三棱锥`S-ABC`中,`SA_|_平面ABC`,`AB_|_BC`,`DE`垂直平分`SC`,且分别交`AC`、`SC`于`D、E`,又`SA=AB=a`,`BC=sqrt(2)a`
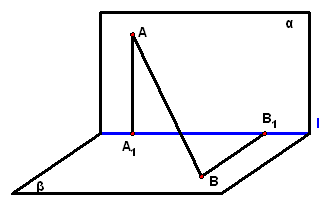
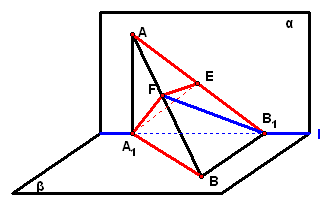
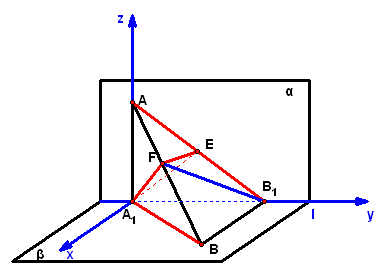
2、(06·陕西19)如图,`alpha_|_beta,alphannbeta=l,Ainalpha,Binbeta`,点`A`在直线`l`上的射影为`A_1`,点`B`在`l`上的射影为`B_1`.已知`AB=2`,`A A_1``=1`,`BB_1`=`sqrt2`,求:
|
|
拓展探究
|
|
|
|
|
学习感悟 二面角的大小是用它的平面角来度量的.找(或作)出二面角的平面角,并且求出其大小,主要有以下几种方法: (2)三垂线法:已知二面角其中一个面内一点到另一个面的垂线,用三垂线定理或其逆定理作平面角. (3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直. (4)射影法:利用面积射影公式`S_射=S_投·costheta`,其中`theta`为平面角的大小,此方法不必在图中画出平面角来. |