2005年
解答题
(17)(本小题满分12分)
已知向量![]() 和
和![]() ,
,
且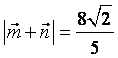 ,求
,求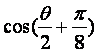 的值
的值![]()
(18) (本小题满分12分)
袋中装有罴球和白球共7个,从中任取2个球都是白球的概率为![]() .现有甲、乙两人
.现有甲、乙两人
从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取![]() 取后不放回,直到两人
取后不放回,直到两人
中有一人取到白球时即终止![]() 每个球在每一次被取出的机会是等可能的,用
每个球在每一次被取出的机会是等可能的,用![]() 表示
表示
取球终止时所需的取球次数.
![]() (Ⅰ)求袋中原有白球的个数;
(Ⅰ)求袋中原有白球的个数;
(Ⅱ)求取球2次终止的概率;
(Ⅲ)求甲取到白球的概率![]()
(19) (本小题满分12分)
已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]()
![]() .
.
(Ⅰ)求m与n的关系表达式;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(20) (本小题满分12分)
如图,已知长方体![]()
![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]()
所成的角为![]() ,
,![]() 垂直
垂直![]() 于
于![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角(锐角)的大小;
所成二面角(锐角)的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离
的距离![]()
(21) (本小题满分12分)已知数列![]() 的首项
的首项![]() 前
前![]() 项和为
项和为![]() ,
,
且![]()
(I)证明数列![]() 是等比数列;
是等比数列;
(II)令![]() ,求函数
,求函数![]() 在点
在点![]() 处的导数
处的导数![]()
(22)
(本小题满分14分)已知动圆过定点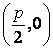 ,且与直线
,且与直线![]() 相切,其中
相切,其中![]() .
.
(I)求动圆圆心![]() 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹![]() 上异于原点
上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的倾斜角分别
的倾斜角分别
为![]() 和
和![]() ,当
,当![]() 变化且
变化且![]() 时,证明直线
时,证明直线![]() 恒过定点,并求出该定点的坐标
恒过定点,并求出该定点的坐标![]()
2006
解答题
(17)(本小题满分12分)
设函数f(x)=![]()
(Ⅰ)求f(x)的单调区间;
(Ⅱ) 讨论f(x)的极值.
18.(本小题满分12分)
已知函数F(x)=Asin2(ωx+φ)(A>0,ω>0,0<φ<![]() ),且y=f(x)的最大值为2,
),且y=f(x)的最大值为2,
其图象相邻两对称轴间的距离为2,并过点(1,2).
(Ⅰ)求φ;
(Ⅱ)计算f(1)+f(2)+…+f(2008).
(19)(本小题满分12分)
盒中装着标有数字1,2,3,4的卡片各2张,从盒中任意任取3张,
每张卡片被抽出的可能性都相等,求:
(Ⅰ)抽出的3张卡片上最大的数字是4的概率;
(Ⅱ)抽出的3张中有2张卡片上的数字是3的概率;
(Ⅲ)抽出的3张卡片上的数字互不相同的概率.
(20) (本小题满分12分)
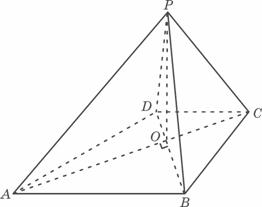 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥CD,AC⊥BD,AC与BD
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥CD,AC⊥BD,AC与BD
相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=![]() ,PB⊥PD.
,PB⊥PD.
(Ⅰ)求异面直线PD与BC所成角的余弦值;
(Ⅱ)求二面角P-AB-C的大小;
(Ⅲ)设点M在棱PC上,且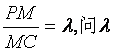 为何值时,PC⊥平面BMD.
为何值时,PC⊥平面BMD.
(21)(本小题满分12分)
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点
所组成的四边形为正方形,两准线间的距离为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)直线l过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,
求直线l的方程.
(22)(本小题满分14分)
已知数列{![]() }中,
}中,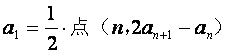 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令![]()
(Ⅱ)求数列![]()
(Ⅲ)设![]()
![]()
![]() 的前n项和。是否存在实数
的前n项和。是否存在实数![]() ,使得
,使得
数列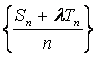 为等差数列?若存在,试求出
为等差数列?若存在,试求出![]() ;若不存在,则说明理由。
;若不存在,则说明理由。
2007年
解答题
17.(本小题满分12分)
在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() .
.
(1)求![]() ;
;
(2)若![]() ,且
,且![]() ,求
,求![]() .
.
18.(本小题满分12分)
设![]() 是公比大于1的等比数列,
是公比大于1的等比数列,![]() 为数列
为数列![]() 的前
的前![]() 项和.已知
项和.已知![]() ,
,
且![]() 构成等差数列.
构成等差数列.
(1)求数列![]() 的等差数列.
的等差数列.
(2)令![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() .
.
19.(本小题满分12分)
 本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用
本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用
不超过9万元,甲、乙电视台的广告收费标准分别为![]() 元/分钟和200元/分钟,规定
元/分钟和200元/分钟,规定
甲、乙两个电视台为该公司所做的每分钟广告,能给公司事来的收益分别为0.3万元
和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益
最大,最大收益是多少万元?
20.(本小题满分12分)
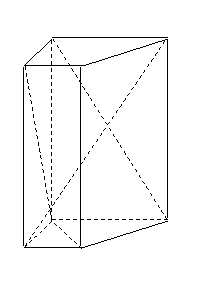
如图,在直四棱柱![]() 中,
中,
已知![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)设![]() 是
是![]() 上一点,试确定
上一点,试确定![]() 的位置,
的位置,
使![]() 平面
平面
![]() ,并说明理由.
,并说明理由.
21.(本小题满分12分)
设函数![]() ,其中
,其中![]() .
.
证明:当![]() 时,函数
时,函数![]() 没有极值点;当
没有极值点;当![]() 时,函数
时,函数![]() 有且只有
有且只有
一个极值点,并求出极值.
22.(本小题满分14分)
已知椭圆![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在![]() 轴上,椭圆
轴上,椭圆![]() 上的点到焦点距离
上的点到焦点距离
的最大值为3,最小值为1.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点(
两点(![]() 不是左右顶点),且以
不是左右顶点),且以![]()
为直径的图过椭圆![]() 的右顶点.求证:直线
的右顶点.求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。