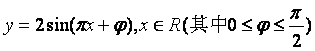解答题

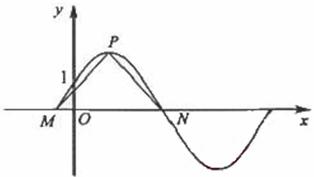
（15）如图，函数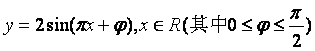的图象与y轴交于点（0，1）

 （Ⅰ）求的值；

       （Ⅱ）设P是图象上的最高点，M、N是图象与x轴的交点，求与的夹角。

      解答

（16）设：

     （Ⅰ）;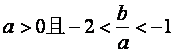

     （Ⅱ）方程在（0，1）内有两个实根。

解答

（17）如图，在四棱锥P-ABCD中，底面为直角梯形，AD//BC，BAD=，

PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点.

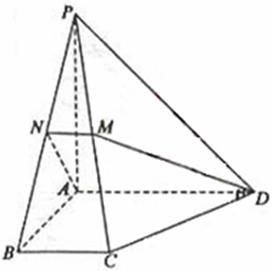
     （Ⅰ）求证：PB⊥DM；

     （Ⅱ） 求CD与平面ADMN所成的角。

 解答

   （18）甲、乙两袋装有大小相同的红球和白球，甲袋装有2个红球，2个白球；

    乙袋装有2个红球，n个白球，现从甲、乙两袋中各任取2个球。

（Ⅰ）若n=3，求取到的4个球全是红球的概率；

（Ⅱ）若取到的4个球中至少有2个红球的概率为，求n.

解答

（19）如图，椭圆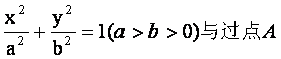（2，0）、B（0，1）

的直线有且只有一个公共点T，且椭圆的离心率e=。

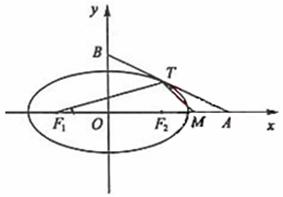
   （Ⅰ）求椭圆方程；

    （Ⅱ）设F₁、F₂分别为椭圆的左、右焦点，M为线段AF₂的中点，

求证：∠ATM=∠AF₁T。

解答

（20）已知函数数列{}（）的第一项以后各项

按如下方式取定：曲线处的切线与经过（0，0）和

（两点的直线平行（如图），求证：当nN⁺时，

（Ⅰ）；

（Ⅱ）。

解答