解答题

(17)（本题满分12分）

已知α是第一象限的角，且cosα=的值.

解答

18．（本题满分12分）

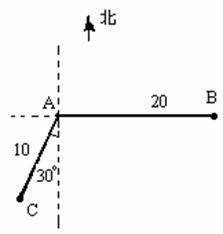
如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘

渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南

偏西30，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向

沿直线前往B处救援（角度精确到1）？

解答

19.（本题满分14分）本题共有2个小题，第1小题满分5分. 第2小题满分9分.

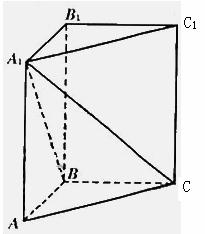
在直三棱柱ABC-A₁B₁C₁中，∠ABC=90°.AB=BC=1，

（1）求异面直线B₁C₁与AC所成角的大小；

（2）若直线A₁C与平面ABC所成角为45°.求三棱柱A₁-ABC的结果.

解答

20(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分.

设数列{a_n}的前n项和为S_n，且对任意正整数n，a_n+S_n=4096.

(1)求数列{a_n}的通项公式：

(2)设数列{log₂a_n}的前n项和为T_n.对数列{T_n}，从第几项起T_n＜-509？

解答

21.(本题满分16分)本题共有3个小题，第4小题满分4分.第2小题满分5分，

第3小题满分7分.

已知在平面直角坐标系xOy中的一个椭圆，它的中心在原点，左焦点为

F（-，0）.且右顶点为D（2，0），设点A的坐标是（1，）.

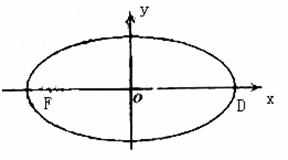
(1)求该椭圆的标准方程.

(2)若P是椭圆上的动点，求线段PA中点M的轨迹方程；

(3)过原点O的直线交椭圆于点B、C.求△ABC面积的最大值.

解答

22．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，

第3小题满分8分.

已知函数y=x＋有如下性质，如果常数a＞0，那么该函数在］上是

减函数，在［，+∞）上是增函数.

（1）如果函数y＝x+在（0，4］上是减函数，在［4，+∞）上是增函数，

求实常数b的值；

（2）设常数c∈[1，4]，求函数f（x）=x+（1≤x≤2）的最大值和最小值；

（3）当n是正整数时，研究函数g（x）=xⁿ-（c＞0）的单调性，并说明理由.

解答