解答题
（17）（本小题满分12分）
设函数f(x)=
(Ⅰ)求f(x)的单调区间；
(Ⅱ) 讨论f(x)的极值.
18.(本小题满分12分)
已知函数F(x)=Asin2(ωx+φ)(A＞0，ω＞0，0＜φ＜
)，且y＝f(x)的最大值为2，
其图象相邻两对称轴间的距离为2，并过点(1，2)．
(Ⅰ)求φ；
(Ⅱ)计算f(1)+f(2)+…+f(2008)．
（19）（本小题满分12分）
盒中装着标有数字1，2，3，4的卡片各2张，从盒中任意任取3张，
每张卡片被抽出的可能性都相等，求：
(Ⅰ)抽出的3张卡片上最大的数字是4的概率；
(Ⅱ)抽出的3张中有2张卡片上的数字是3的概率；
(Ⅲ)抽出的3张卡片上的数字互不相同的概率.
(20) （本小题满分12分）
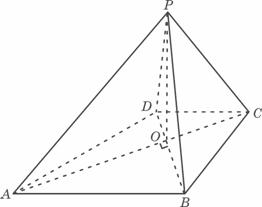如图，已知四棱锥P-ABCD的底面ABCD为等腰梯形，AB∥CD,AC⊥BD,AC与BD
相交于点O，且顶点P在底面上的射影恰为O点，又BO=2,PO=
,PB⊥PD.
(Ⅰ)求异面直线PD与BC所成角的余弦值；
(Ⅱ)求二面角P-AB-C的大小；
(Ⅲ)设点M在棱PC上，且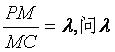
为何值时，PC⊥平面BMD.
（21）（本小题满分12分）
已知椭圆的中心在坐标原点O，焦点在x轴上，椭圆的短轴端点和焦点
所组成的四边形为正方形，两准线间的距离为4.
(Ⅰ)求椭圆的方程；
(Ⅱ)直线l过点P(0,2)且与椭圆相交于A、B两点，当ΔAOB面积取得最大值时，
求直线l的方程.
（22）（本小题满分14分）
已知数列｛
｝中，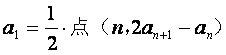
在直线y=x上，其中n=1,2,3….
(Ⅰ)令
(Ⅱ)求数列
(Ⅲ)设
的前n项和。是否存在实数
，使得
数列
为等差数列？若存在，试求出
；若不存在，则说明理由。