解答题

17.(本小题满分12分)

   已知函数F(x)=Asin²(ωx+φ)(A＞0，ω＞0，0＜φ＜)，且y＝f(x)的最大值为2，

其图象相邻两对称轴间的距离为2，并过点(1，2)．

   (Ⅰ)求φ；

   (Ⅱ)计算f(1)+f(2)+…+f(2008)．

解答

18．(本小题满分12分)

    设函数f(x)=ax-(a+1)ln(x+1)，其中a≥-1．求f(x)的单调区间．

解答

19.(本小题满分12分)

   如图，已知平面A₁B₁C₁平行于三棱锥V-ABC的底面ABC，等边△AB₁C

所在的平面与底面ABC垂直，且∠ACB＝90°．设AC＝2a，BC＝a．

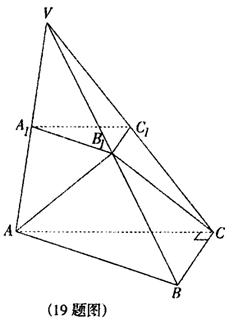
   (Ⅰ)求证直线B₁C₁是异面直线AB₁与A₁C₁的公垂线；

   (Ⅱ)求点A到平面VBC的距离；

   (Ⅲ)求二面角A-VB-C的大小．

解答

20.(本小题满分12分)

    袋中装着标有数字1，2，3，4，5的小球各2个．从袋中任取3个小球，

按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，

用ξ表示取出的3个小球上的最大数字，求：

    (Ⅰ)取出的3个小球上的数字互不相同的概率；

    (Ⅱ)随机变量ξ的概率分布和数学期望；

    (Ⅲ)计分介于20分到40分之间的概率．

解答

21.（本小题满分12分）

      双曲线C与椭圆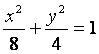有相同的焦点，直线y=x为C的一条渐近线．

     （Ⅰ）求双曲线C的方程；

     （Ⅱ）过点P（0，4）的直线l，交双曲线C于A、B两点，交x轴于Q点

（Q点与C的顶点不重合）.当=λ₁=λ₂，且λ₁+λ₂=时，求Q点的坐标．

解答

22.(本小题满分14分)

    已知a₁＝2，点(a_n，a_n+1)在函数f(x)=x²+2x的图象上，其中n=1，2，3，…．

(Ⅰ)证明数列{lg(1+a_n)}是等比数列；

(Ⅱ)设T_n=(1+a₁)(1+a₂)…(1+a_n)，求T_n及数列{a_n}的通项；

(Ⅲ)记b_n=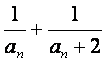，求数列{b_n}的前n项和S_n,并证明S_n+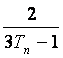=1.

解答