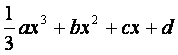 ,其中a
, b , c是以d为公差的等差数列,,
,其中a
, b , c是以d为公差的等差数列,,三、解答题
21.(本小题满分12分)
已知函数f(x)=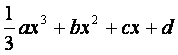 ,其中a
, b , c是以d为公差的等差数列,,
,其中a
, b , c是以d为公差的等差数列,,
且a>0,
d>0.设![]() [1-
[1-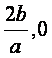 ]上,
]上,![]() 在
在![]() 处取得
处取得
最大值,在![]() ,将点
,将点![]() 依次记为A,
依次记为A,
B,
C.![]()
( = 1 \* ROMAN I)求![]()
( = 2 \* ROMAN II)若⊿ABC有一边平行于x轴,且面积为![]() ,求a
,d的值
,求a
,d的值
本小题考查函数的导数,函数极值的判定,闭区间上二次函数的最值,等差数
列等基础知识的综合运用,考查用数形结合的数学思想分析问题,解决问题的能力,
满分12分.
(Ⅰ)解:∵2b=a+c.
∴f′(x)=ax2+2bx+c=ax2+(a+c)x+c=(x+1)(ax+c).
令f′(x)=0,得x=-1,或x=
-![]()
∵a>0,d>0,
∴0<a<b<c,
∴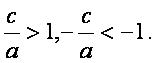
当![]() <x<-1时,f′(x)<0,
<x<-1时,f′(x)<0,
当x>-1时,f′(x)>0,
所以f(x)在x= -1处取得极小值,即
x0= -1.
(Ⅱ)解法一:∵f′(x)=ax2+2bx+c,a>0.
∴f′(x)的图象开口向上,对称轴方程是x=
-![]()
由![]() >1,知
>1,知
∴f′(x)在[1-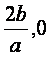 ]上的最大值为f′(0)=c,即
]上的最大值为f′(0)=c,即
x1=0.
又由![]() >1,知-
>1,知-![]() ∈[1-
∈[1-![]() ],
],
∴当x=
-![]() 时,f′(x)取得最小值f′(-
时,f′(x)取得最小值f′(-![]() )=-
)=-![]() 即
即
x2=-![]() .
.
∵f(x0)=f(-1)=
-![]()
∴A(-1,-![]() ),B(0,c),C(-
),B(0,c),C(-![]() ,-
,-![]() ).
).
由△ABC有一条边平行于x轴,得AC平行于x轴,所以
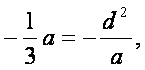 即
即
a2=3d2. ①
又由△ABC的面积为2+![]() ,得
,得
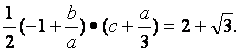
利用b=a+d,c=a+2d,得
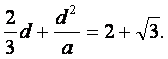 ②
②
联立①,②可得
d=3,a=3![]() .
.
解法二:∵f′(x)=ax2+2bx+c,a>0,
f′(1-![]() )=0,f′(0)=c.
)=0,f′(0)=c.
由c>0知f′(x)在[1-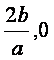 ]上的最大值为f′(0)=c.即
]上的最大值为f′(0)=c.即
x1=0.
由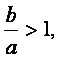 知-
知-![]() ∈[1-
∈[1-![]() ].
].
∴当x=
-![]() 时f′(x)取得最小值f′(-
时f′(x)取得最小值f′(-![]() )=
-
)=
-![]() 即
即
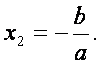
∵f(x0)=f(-1)=-![]()
∴A(-1,-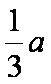 ),B(0,c),C(-
),B(0,c),C(-![]() ,-
,-![]() ).
).
由△ABC有一条边平行于x轴,得AC平行于x轴,所以
-![]() =
-
=
-![]() ,即
,即
a2=3d2. ①
又由△ABC的面积为2+![]() ,得
,得
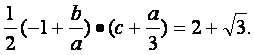
利用b=a+d,c=a+2d,得
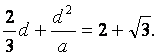 ②
②
联立①,②可得
d=3,a=3![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。