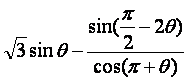16．(本小题满分12分)

    已知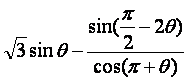·cosθ=1,θ∈(0，π)，求θ的值．

解答

17．(本小题满分12分)

    某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)．若安检不合格，

则必须整改．若整改后经复查仍不合格，则强制关闭．设每家煤矿安检是否合格

是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率

是0.8，计算(结果精确到0.01)：

    (Ⅰ)恰好有两家煤矿必须整改的概率；

    (Ⅱ)平均有多少家煤矿必须整改；

    (Ⅲ)至少关闭一家煤矿的概率．

解答

18．(本小题满分14分)

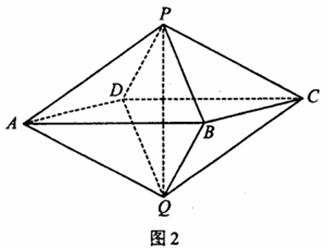
    如图2，已知两个正四棱锥P-ABCD与Q-ABCD的高都为2，AB=4．

    (Ⅰ)证明PQ⊥平面ABCD；

    (Ⅱ)求异面直线AQ与PB所成的角；

    (Ⅲ)求点P到平面QAD的距离．

      解答

19．(本小题满分14分)

    已知函数f(x)=ax³-3x²+1-.

    (Ⅰ)讨论函数f(x)的单调性；

    (Ⅱ)若曲线y=f(x)上两点A、B处的切线都与y轴垂直，且线段AB与x轴有公共点，

求实数a的取值范围.

解答

20．(本小题满分14分)

    在m(m≥2)个不同数的排列p₁p₂…p_m中，若1≤i＜j≤m时p_i＞p_j (即前面某数大

于后面某数)，则称与构成一个逆序．一个排列的全部逆序的总数称为该排列的逆

序数．记排列(n+1)n(n-1)…321的逆序数为，如排列21的逆序数=1，排列321的逆

序数=3，排列4321的逆序数=6．

    (Ⅰ)求、，并写出的表达式；

(Ⅱ)令=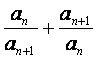,证明  2n＜++…+＜2n+3， n=1，2，…．

解答

21.（本小题满分14分）

已知椭圆C₁∶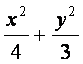=1，抛物线C₂∶（y-m）²=2px（p＞0），且C₁、C₂的公共弦AB

过椭圆C₁的右焦点.

(Ⅰ)当AB⊥x轴时，求p、m的值，并判断抛物线C₂的焦点是否在直线AB上；

(Ⅱ)若P=且抛物线C₂的焦点在直线AB上，求m的值及AB的方程．

解答