解答题

16．（本小题满分12分）

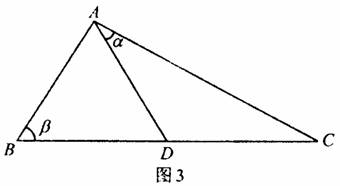
如图3，D是直角△ABC斜边BC上一点，AB=AD，记∠CAD=α，∠ABC=β.

（Ⅰ）证明：sinα+cos2β=0；

（Ⅱ）若AC=DC，求β的值.

解答

17．(本小题满分12分)

    某安全生产监督部门对5家小型煤矿进行安全检查(简称安检)．若安检不合格，

则必须整改．若整改后经复查仍不合格，则强制关闭．设每家煤矿安检是否合格

是相互独立的，且每家煤矿整改前安检合格的概率是0.5，整改后安检合格的概率

是0.8，计算(结果精确到0.01)：

    (Ⅰ)恰好有两家煤矿必须整改的概率；

    (Ⅱ)平均有多少家煤矿必须整改；

    (Ⅲ)至少关闭一家煤矿的概率．

解答

18．(本小题满分14分)

    如图4，己知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2，AB=4．

    (Ⅰ)证明PQ⊥平面ABCD；

    (Ⅱ)求异面直线AQ与PB所成的角；

    (Ⅲ)求点P到平面QAD的距离．

解答     

19．(本小题满分14分)

已知函数f(x)=x-sinx，数列{a_n}满足：0＜a₁＜1，a_n+1=f(a_n)，n=1，2，3，…．

证明：(Ⅰ)0＜a_n+1＜a_n＜1；(Ⅱ)a_n+1＜a_n³．

解答

20．(本小题满分14分)

对1个单位质量的含污物体进行清洗，清洗前其清洁度(含污物体的清洁度定义为：

1-)为0.8，要求洗完后的清洁度是0.99．有两种方案可供选择，方案

甲：一次清洗；方案乙：分两次清洗．该物体初次清洗后受残留水等因素影响，其

质量变为a(1≤a≤3)．设用x单位质量的水初次清洗后的清洁度是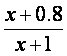(x＞a-1)，用

y单位质量的水第二次清洗后的清洁度是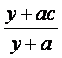，其中c(0.8＜c＜0.99)是该物体初次清

洗后的清洁度．

(Ⅰ)分别求出方案甲以及c=0.95时方案乙的用水量，并比较哪一种方案用水量较少；

(Ⅱ)若采用方案乙，当a为某定值时，如何安排初次与第二次清洗的用水量，使总用水

量最少?并讨论a取不同数值时对最少总用水量多少的影响．

解答

21.(本小题满分14分)

已知椭圆C₁: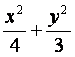=1，抛物线C₂:(y-m)²=2px(p＞0)，且C₁、C₂的公共弦AB过椭圆

C₁的右焦点.

(Ⅰ)当AB⊥x轴时，求m、p的值，并判断抛物线C₂的焦点是否在直线AB上；

(Ⅱ)是否存在m、p的值，使抛物线C₂的焦点恰在直线AB上?若存在，求出符合条件的

m、p的值；若不存在，请说明理由．

解答