解答题
全国卷Ⅰ(理)
(20)(本小题满分12分)
在平面直角坐标系xOy中,有一个以![]() 和
和![]() 为焦点、离心率为
为焦点、离心率为![]() 的
的
椭圆,设椭圆在第一象限的部分为曲线C,动点P在C上,C在点P处的切线与x、y轴的
交点分别为A、B,且向量![]() ,求:
,求:
(Ⅰ)点M的轨迹方程;
(Ⅱ)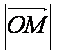 的最小值。
的最小值。
全国卷Ⅱ(理)
(20)(本小题满分12分)
设函数![]() 若对所有的
若对所有的![]() 都有
都有![]() 成立,
成立,
求实数![]() 的取值范围。
的取值范围。
北京卷(理)
(18)(本小题共13分)
某公司招聘员工,指定三门考试课程,有两种考试方案.
方案一:考试三门课程,至少有两门及格为考试通过;
方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.
假设某应聘者对三门指定课程考试及格的概率分别是a,b,c,且三门课程
考试是否及格相互之间没有影响.
(Ⅰ)分别求该应聘者用方案一和方案二时考试通过的概率;
(Ⅱ)试比较该应聘者在上述两种方案下考试通过的概率的大小.(说明理由)
天津卷(理)
(20)(本小题满分12分)
已知函数f(x)=4x3-3x2cosθ+![]() cosθ,其中x∈R,θ为参数,且0≤θ<2π.
cosθ,其中x∈R,θ为参数,且0≤θ<2π.
(Ⅰ)当cosθ=0时,判断函数f(x)是否有极值;
(Ⅱ)要使函数f(x)的极小值大于零,求参数θ的取值范围;
(Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ,函数f(x)在区间
(2a-1,a)内都是增函数,求实数α的取值范围.
上海卷(理)
20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分)
在平面直角坐标系![]() O
O![]() 中,直线
中,直线![]() 与抛物线
与抛物线![]() =2
=2![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线![]() 过点T(3,0),那么
过点T(3,0),那么![]()
![]() =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.
辽宁卷
(20) (本小题满分14分)
已知点![]() ,
,![]()
![]() 是抛物线
是抛物线![]() 上的两个动点,
上的两个动点,![]() 是坐
是坐
标原点,向量![]() ,
,![]() 满足
满足![]() .设圆
.设圆![]() 的方程为
的方程为
![]()
(I)
证明线段![]() 是圆
是圆![]() 的直径;
的直径;
(II)当圆C的圆心到直线X-2Y=0的距离的最小值为时,求P的值。
江苏卷
(20)(本小题满分16分,第一小问4分,第二小问满分6分,第三小问满分6分)
设a为实数,设函数![]() 的最大值为g(a)。
的最大值为g(a)。
(Ⅰ)设t=![]() ,求t的取值范围,并把f(x)表示为t的函数m(t)
,求t的取值范围,并把f(x)表示为t的函数m(t)
(Ⅱ)求g(a)
(Ⅲ)试求满足![]() 的所有实数a
的所有实数a
浙江卷(理)
(18)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;
乙袋装有2个红球,n个白球,现从甲、乙两袋中各任取2个球。
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为![]() ,求n.
,求n.
福建卷(理)
(20)(本小题满分12分)
已知椭圆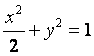 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O、F,并且与椭圆的左准线![]() 相切的圆的方程;
相切的圆的方程;
(II)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分
线与![]() 轴交于点G,求点G横坐标的取值范围。
轴交于点G,求点G横坐标的取值范围。
湖北卷(理)
19.(本小题满分10分)
在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似服从正态分布N(70,100)。
已知成绩在90分以上(含90分)的学生有12名。
(Ⅰ)试问此次参赛的学生总数约为多少人?
(Ⅱ)若该校计划奖励竞赛成绩排在前50名的学生,试问设奖的分数线约为多少分?
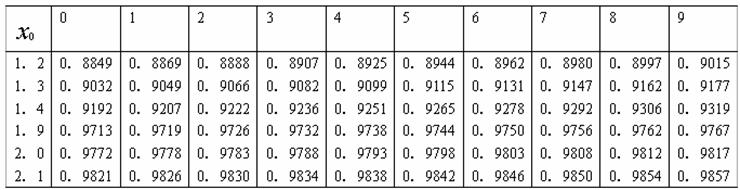
可供查阅的(部分)标准正态分布表![]() (x0)=P(x<x0)
(x0)=P(x<x0)
湖南卷(理)
19.(本小题满分14分)
已知函数f(x)=x-sinx,数列{an}满足:0<a1<1,an+1=f(an),n=1,2,3,….
证明:(Ⅰ)0<an+1<an<1;(Ⅱ)an+1<![]() an3.
an3.
广东卷
18.(本小题满分14分)
设函数f(x)=-x3+3x+2分别在x1、x2处取得极小值、极大值。xoy平面
上点A、B的坐标分别为(x1,f(x1))、(x2,f(x2))。该平面上动点P满
足![]() ,点Q是点P关于直线y=2(x-4)的对称点,求:
,点Q是点P关于直线y=2(x-4)的对称点,求:
(Ⅰ)点A、B的坐标:
(Ⅱ)动点Q的轨迹方程。
重庆卷(理)
(20)(本小题满分13分)
已知函数![]() ,其中
,其中![]() 为常数。
为常数。
(Ⅰ)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,且
,且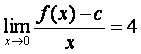 ,试证:
,试证:![]() ;
;
山东卷(理)
20.(本小题满分12分)
袋中装着标有数字1,2,3,4,5的小球各2个.从袋中任取3个小球,
按3个小球上最大数字的9倍计分,每个小球被取出的可能性都相等,
用ξ表示取出的3个小球上的最大数字,求:
(Ⅰ)取出的3个小球上的数字互不相同的概率;
(Ⅱ)随机变量ξ的概率分布和数学期望;
(Ⅲ)计分介于20分到40分之间的概率.
江西卷(理)
20.(本小题满分12分)
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,
且AD=![]() ,BD=CD=1.另一个侧面ABC是正三角形.
,BD=CD=1.另一个侧面ABC是正三角形.
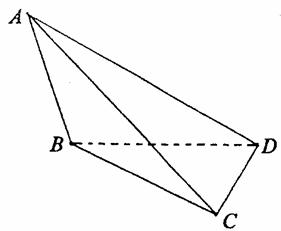
(1)求证:AD⊥BC;
(2)求二面角B-AC-D的大小;
(3)在线段AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定点E的位置;
若不存在,说明理由.
陕西卷(理)
(20)(本小题12分)
已知正项数列![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() 且
且![]() 成等比
成等比
数列,求数列![]() 的通项
的通项![]()
四川卷(理)
(20)(本大题满分12分)
如图,在长方体![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,
![]() 分别是
分别是![]() 的中点,
的中点,![]()
(Ⅰ)求证:![]() 面
面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
安徽卷(理)
(20)(本小题满分12分)
已知函数f(x)在R上有定义,对任意实数a>0和任意实数x,都有
![]()
(Ⅰ)证明f(0)=0:
(Ⅱ)证明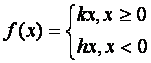 ,其中k和h均为常数:
,其中k和h均为常数:
(Ⅲ)当(Ⅱ)中的k>0,设g(x)=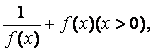 讨论g(x)在(0,+
讨论g(x)在(0,+![]() )内
)内
的单调性并求极值。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。