解答题
15.(本小题满分14分)
已知函数![]()
(Ⅰ)求f(x)的最小正周期:![]()
(Ⅱ)求f(x)的最大值和最小值:
(Ⅲ)若![]() 求sin2
求sin2![]() 的值。
的值。
16.(本小题满分12分)
某运动员射击一次所得环数X的分布如下:
|
X |
0-6 |
7 |
8 |
9 |
10 |
|
p |
0 |
0.2 |
0.3 |
0.3 |
0.2 |
现进行两次射击,以该运动员两次射击中最高环数作为他的成绩,记为![]() 。
。
(Ⅰ)求该运动员两次都命中7环的概率:
(Ⅱ)求![]() 的分布列:
的分布列:
(Ⅲ)求![]() 的数学期望E
的数学期望E![]() 。
。
17.(本小题满分14分)
如图所示,AF、DE分别是⊙![]() 、⊙
、⊙![]() 1的直径。AD与两圆所在的平面均
1的直径。AD与两圆所在的平面均
垂直,AD=8,BC是⊙![]() 的直径,AB=AC=6,OE//AD。
的直径,AB=AC=6,OE//AD。
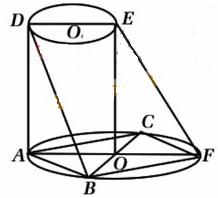
(Ⅰ)求二面角B-AD-F的大小;
(Ⅱ)求直线BD与EF所成的角。
18.(本小题满分14分)
设函数f(x)=-x3+3x+2分别在x1、x2处取得极小值、极大值。xoy平面
上点A、B的坐标分别为(x1,f(x1))、(x2,f(x2))。该平面上动点P满
足![]() ,点Q是点P关于直线y=2(x-4)的对称点,求:
,点Q是点P关于直线y=2(x-4)的对称点,求:
(Ⅰ)点A、B的坐标:
(Ⅱ)动点Q的轨迹方程。
19.(本小题满分14分)
已知公比为q(0<q<1)的无穷等比数列{an}各项的和为9,无穷等比
数列{an2}各项的和为![]() 。
。
(Ⅰ)求数列{an}的首项a1和公比q:
(Ⅱ)对给定的k(k=1,2,…,n),设T{k}是首项为ak,公差为2ak-1的
等差数列,求数列T{2}的前10项之和:
(Ⅲ)设bi为数列![]() 的第i项,sn=b1+b2+…+bn,求sn,并求正整数
的第i项,sn=b1+b2+…+bn,求sn,并求正整数
m(m>1),使得![]()
![]() 存在且不等于零。
存在且不等于零。
(注:无穷等比数列各项的和即当n![]() 时该无穷等比数列前n项和的极限)
时该无穷等比数列前n项和的极限)
20.(本小题满分12分)
A是由定义在[2,4]上且满足如下条件的函数![]() (x)组成的集合:
(x)组成的集合:
①对任意的![]() 都有
都有![]() (2x)
(2x)![]() ;②存在常数L(0<L<1),
;②存在常数L(0<L<1),
使得对任意的x1,x2![]() [1,2],都有|
[1,2],都有|![]() (2x1)-
(2x1)-![]() (2x2)|
(2x2)|![]() .
.
(Ⅰ)设![]() (x)=
(x)=![]() 证明:
证明:![]() (x)
(x)![]() A:
A:
(Ⅱ)设![]() (x)
(x)![]() ,如果存在x0
,如果存在x0![]() (1,2),使得x0=
(1,2),使得x0=![]() (2x0),
(2x0),
那么这样的x0是唯一的:
(Ⅲ)设![]()
![]() 任取x1
任取x1![]() (1,2),令xn+1=
(1,2),令xn+1=![]() (2xn),n=1,2……证明:给定
(2xn),n=1,2……证明:给定
正整数k,对任意的正整数p,成立不等式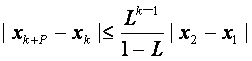 。
。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。