解答题
(17)(本小题满分12分)
已知函数![]()
(I)求函数![]() 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(II)函数![]() 的图象可以由函数
的图象可以由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
(18)(本小题满分12分)
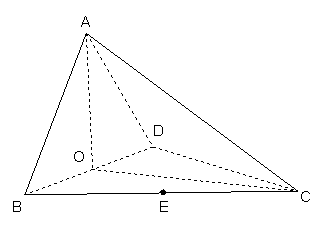
如图,四面体ABCD中,O、E分别是BD、BC的中点,
![]()
(I)求证:![]() 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。
(19)(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量![]() (升)关于行驶
(升)关于行驶
速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:
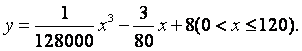 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(20)(本小题满分12分)
已知椭圆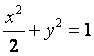 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
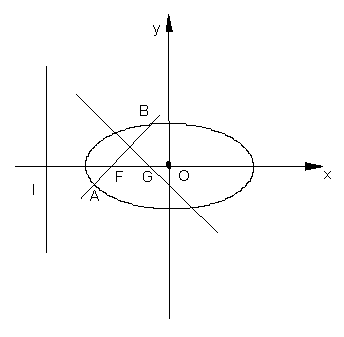
(I)求过点O、F,并且与椭圆的左准线![]() 相切的圆的方程;
相切的圆的方程;
(II)设过点F且不与坐标轴垂直的直线交椭圆于A、B两点,线段AB的垂直平分
线与![]() 轴交于点G,求点G横坐标的取值范围。
轴交于点G,求点G横坐标的取值范围。
(21)(本小题满分12分)
已知函数![]()
(I)求![]() 在区间
在区间![]() 上的最大值
上的最大值![]()
(II)是否存在实数![]() 使得
使得![]() 的图象与
的图象与![]() 的图象有且只有三
的图象有且只有三
个不同的交点?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(22)(本小题满分14分)
已知数列![]() 满足
满足![]()
(I)求数列![]() 的通项公式;
的通项公式;
(II)
若数列|bn|满足![]() ,
,
证明:|bn|是等差数列
(Ⅲ)证明: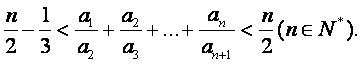
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。