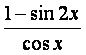解答题

(15)(本小题共12分)

已知函数f(x)=.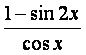

(Ⅰ)求f(x)的定义域；

(Ⅱ)设α是第四象限的角，且tanα= -，求f(α)的值.

解答

(16)(本小题共13分)

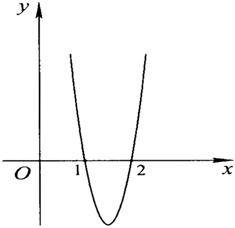
已知函数f(x)=ax³+bx²+cx在点x₀处取得极大值5，其导函数y=f′(x)的图象经

过点(1，0)，(2，0)，如图所示.求：

(Ⅰ)x₀的值；

(Ⅱ)a，b，c的值.

解答

(17)(本小题共14分)

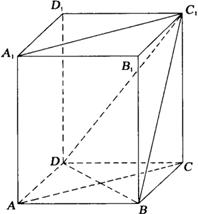
如图，ABCD-A₁B₁C₁D₁是正四棱柱.

(Ⅰ)求证：BD⊥平面ACC₁A₁；

(Ⅱ)若二面角C₁-BD-C的大小为60°，求异面直线BC₁与AC所成角的大小.

解答

(18)(本小题共13分)

    某公司招聘员工，指定三门考试课程，有两种考试方案．

    方案一：考试三门课程，至少有两门及格为考试通过：

    方案二：在三门课程中，随机选取两门，这两门都及格为考试通过．

    假设某应聘者对三门指定课程考试及格的概率分别是0．5，0．6，0．9，

且三门课程考试是否及格相互之间没有影响．求：

(Ⅰ)该应聘者用方案一考试通过的概率；

(Ⅱ)该应聘者用方案二考试通过的概率．

解答

(19)(本小题共14分)

椭圆C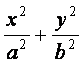：=1(a＞b＞0)的两个焦点为F₁，F₂，点P在椭圆C上，且

PF₁⊥F₁F₂，|PF₁|=，|PF₂|=.

(Ⅰ)求椭圆C的方程；

(Ⅱ)若直线l过圆x²+y²+4x-2y=0的圆心M，交椭圆C于A，B两点，且A，B

关于点M对称，求直线l的方程.

 解答

(20)(本小题共14分)

设等差数列{a_n}的首项a₁及公差d都为整数，前n项和为S_n.

(Ⅰ)若a₁₁=0，S₁₄=98，求数列{a_n}的通项公式；

(Ⅱ)若a₁≥6，a₁₁＞0，S₁₄≤77，求所有可能的数列{a_n}的通项公式.

解答