解答题
(17)(本小题满分12分)
在![]() 中,
中,![]() 所对的边长分别为
所对的边长分别为![]() ,设
,设![]() 满足条件
满足条件
![]() 和
和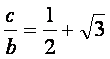 ,求
,求![]() 和
和![]() 的值
的值
(18)(本小题满分12分)
已知![]()
![]()
(Ⅰ)当![]() 时,求数列
时,求数列![]() 的前n项和
的前n项和![]()
(Ⅱ)求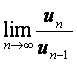
(19)(本小题满分12分)
如图,在斜三棱柱![]() 中,
中,![]() ,
,
侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E、F分别是棱
,E、F分别是棱![]() 的中点
的中点
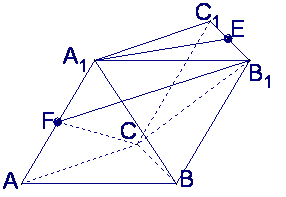 (Ⅰ)求
(Ⅰ)求![]() 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明![]() ∥平面
∥平面![]()
(Ⅲ)求经过![]() 四点的球的体积
四点的球的体积
(20)(本小题满分12)
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),
塔所在的山高OB=220(米),OA=200(米),
图中所示的山坡可视为直线![]() 且点P在直线
且点P在直线![]() 上,
上,
![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,tan
,tan![]() =1/2试问此人
=1/2试问此人
距水平地面多高时,观看塔的视角∠BPC最大
(不计此人的身高)
(21)(本小题满分14分)
抛物线C的方程为![]() ,过抛物线C上一点P(x0,y0)(x0≠0)作斜率
,过抛物线C上一点P(x0,y0)(x0≠0)作斜率
为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互
不相同),且满足![]()
![]()
(Ⅰ)求抛物线C的焦点坐标和准线方程
(Ⅱ)设直线AB上一点M,满足![]() ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上
(Ⅲ)当![]() =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
![]() 的取值范围
的取值范围
(22)(本小题满分14分)
设函数![]() .
.
(Ⅰ)证明![]() ,其中为k为整数;
,其中为k为整数;
(Ⅱ)设![]() 为
为![]() 的一个极值点,证明
的一个极值点,证明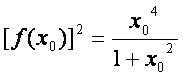 ;
;
(Ⅲ)设![]() 在(0,+∞)内的全部极值点按从小到大的顺序排列
在(0,+∞)内的全部极值点按从小到大的顺序排列![]() ,
,
证明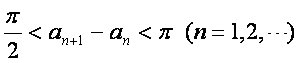
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。