解答题

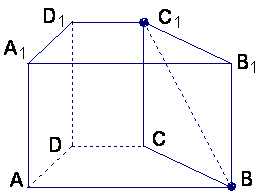
17.已知直四棱柱中，，底面是直角梯形，

，，，，，求异面直线与

所成的角的大小（结果用反三角函数表示）

解答

18.证明：在复数范围内，方程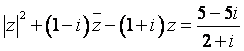（为虚数单位）无解

解答

19.点A、B分别是椭圆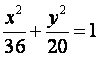长轴的左、右焦点，点F是椭圆的右焦点点P在椭圆上，

且位于x轴上方，

（1）求P点的坐标；

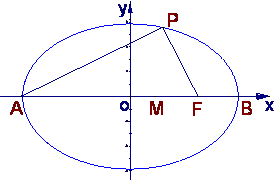    （2）设M是椭圆长轴AB上的一点，M到直线AP的

     距离等于，求椭圆上的点到点M的距离d的最小值

解答

20.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分

假设某市2004年新建住房400万平方米，其中有250万平方米是中低价房预计

在今后的若干年内，该市每年新建住房面积平均比上一年增长8%，另外，每年新

建住房中，中低价房的面积均比上一年增加50万平方米那么，到那一年底，

（1）该市历年所建中低价房的累计面积（以2004年为累计的第一年）将首次不少

于4750万平方米？

（2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？

解答

21.（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分8分，

第3小题满分6分

对定义域是.的函数.，

规定：函数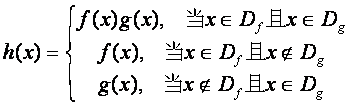

（1）若函数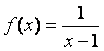，，写出函数的解析式；

（2）求问题（1）中函数的值域；

（3）若，其中是常数，且，请设计一个定义域为R的函数

，及一个的值，使得，并予以证明

解答

22.在直角坐标平面中，已知点，，，，其中

n是正整数对平面上任一点，记为关于点的对称点，为关于点的

对称点，为关于点的对称点

（1）求向量的坐标；

（2）当点在曲线C上移动时，点的轨迹是函数的图像，其中是

以3位周期的周期函数，且当时，求以曲线C为图像的函数

在上的解析式；

（3）对任意偶数n，用n表示向量的坐标

解答