解答题
17.(本小题满分12分)
甲.乙.丙三台机器是否需要照顾相互之间没有影响![]() 已知在某一个小时内,甲.乙
已知在某一个小时内,甲.乙
都需要照顾的概率是0.05,甲.丙都需要照顾的概率是0.05,乙.丙都需要照顾的
概率是0.125![]()
1)求甲.乙.丙三台机器在这一个小时内各自需要照顾的概率?
2)计算在这一个小时内至少有一台需要照顾的概率?
18.(本小题满分12分)
四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,
平面VAD⊥底面ABCD![]()
 1)求证AB⊥面VAD;
1)求证AB⊥面VAD;
2)求面VAD与面VDB所成的二面角的大小.
19.(本小题满分12分)
![]() 中,内角
中,内角![]() .
.![]() .
.![]() 的对边分别为
的对边分别为![]() .
.![]() .
.![]() ,已知
,已知![]() .
.![]() .
.![]() 成等比数列,且
成等比数列,且![]()
![]()
![]()
(1)求![]() 的值;
的值;
(2)若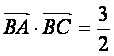 ,求
,求![]() 的值
的值![]()
20.(本小题满分12分)
在等差数列{an}中,公差d≠0,且a2是a1和a4的等比中项,已知a1,a3,![]()
成等比数列,求数列k1,k2,k3,…,kn的通项kn![]()
21.(本小题满分14分)
设![]() .
.![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是
是![]() 的垂直平分线
的垂直平分线![]()
1)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点
经过抛物线的焦点![]() ?证明你的结论;
?证明你的结论;
2)当直线![]() 的斜率为2时,求
的斜率为2时,求![]() 在
在![]() 轴上截距的取值范围
轴上截距的取值范围![]()
22.(本小题满分12分)
已知函数f(x)=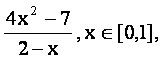
(1)求函数f(x)的单调区间和值域;
(2)设a≥1, 函数g(x)=x3-3a2x-2a, x∈[0,1], 若对于任意x1∈[0,1],
总存在x0∈[0,1],
使得g((x0)
=f(x1)成立,求a的取值范围![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。