解答题

（17）（本小题满分12分）

设函数，求使的取值范围．

解答

（18） （本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…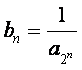

（Ⅰ）证明为等比数列；

（Ⅱ）如果无穷等比数列各项的和，求数列的首项和公差．

（注：无穷数列各项的和即当时数列前项和的极限）

解答

（19）（本小题满分12分）

甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.6，

本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没

有影响．令为本场比赛的局数．求的概率分布和数学期望．（精确到0.0001）

解答

（20）（本小题满分12分）

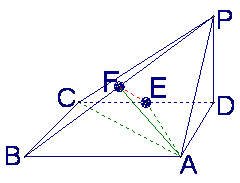     如图，四棱锥P-ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD，E、F分别

     为CD、PB的中点．

    （Ⅰ）求证：EF垂直于平面PAB；

    （Ⅱ）设AB=BC，求AC与平面AEF所成的角的大小．

解答

（21）（本小题满分14分）

P、Q、M、N四点都在椭圆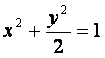上，F为椭圆在y轴正半轴上的焦点．已知

与共线，与共线，且．求四边形PMQN的面积的最小值和最大值．

解答

（22）（本小题满分12分）

已知，函数．

（Ⅰ）当x为何值时，f(x)取得最小值？证明你的结论；

（Ⅱ）设f(x)在[-1,1]上是单调函数，求a的取值范围．

解答