解答题

全国卷Ⅰ(理)

（20）（本大题满分12分）

9粒种子分种在3个坑内，每坑3粒，每粒种子发芽的概率为，若一个坑内至少

有1粒种子发芽，则这个坑不需要补种; 若一个坑内的种子都没发芽，则这个坑

需要补种假定每个坑至多补种一次，每补种1个坑需10元，用ξ表示补种费用，

写出ξ的分布列并求ξ的数学期望（精确到）

 解答

全国卷Ⅱ(理)

（20）（本小题满分12分）

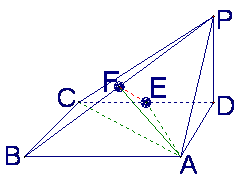     如图，四棱锥P-ABCD中，底面ABCD为矩形，PD垂直于底面ABCD，AD=PD，E、F分别

     为CD、PB的中点．

    （Ⅰ）求证：EF垂直于平面PAB；

    （Ⅱ）设AB=BC，求AC与平面AEF所成的角的大小．

解答

全国卷Ⅲ(理)

20.（本小题满分12分）

    在等差数列{an}中，公差d≠0,且a2是a1和a4的等比中项,已知a1,a3,

成等比数列，求数列k1,k2,k3,…,kn的通项kn 

解答

北京卷(理)

18 (本小题共14分)

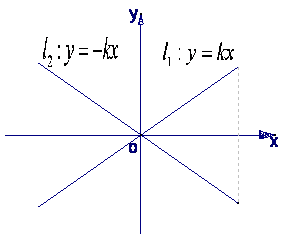     如图,直线与直线之间的阴影区域(不含边界)记为,

     其左半部分记为,右半部分记为

      (Ⅰ)分别有不等式组表示和

      (Ⅱ)若区域中的动点到的距离

     之积等于,求点的轨迹的方程;

      (Ⅲ)设不过原点的直线与(Ⅱ)中的曲线

     相交于两点,且与分别交于两点.

     求证△的重心与△的重心重合

解答

天津卷(理)

（20）（本小题满分12）

    某人在一山坡P处观看对面山项上的一座铁塔，如图所示，塔高BC=80（米），

    塔所在的山高OB=220（米），OA=200（米），

    图中所示的山坡可视为直线且点P在直线上，

    与水平地面的夹角为 ,tan=1/2试问此人

    距水平地面多高时，观看塔的视角∠BPC最大

   （不计此人的身高） 

解答

上海卷(理)

20.（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分

假设某市2004年新建住房400万平方米，其中有250万平方米是中低价房预计

在今后的若干年内，该市每年新建住房面积平均比上一年增长8%，另外，每年新

建住房中，中低价房的面积均比上一年增加50万平方米那么，到那一年底，

（1）该市历年所建中低价房的累计面积（以2004年为累计的第一年）将首次不少

于4750万平方米？

（2）当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%？

解答

辽宁卷

 20．（本小题满分12分）

 某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，

 两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对

 每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品.

   （Ⅰ）已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示，

    分别求生产出的甲、乙产品为一等品的概率P甲、P乙；

   （Ⅱ）已知一件产品的利润如表二所示，用ξ、

         η分别表示一件甲、乙产品的利润，在

        （I）的条件下，求ξ、η的分布列及

Eξ、Eη；

   （Ⅲ）已知生产一件产品需用的工人数和资金额

         如表三所示.该工厂有工人40名，可用资

         品的数量，在（II）的条件下，x、y为何

         值时，最大？最大值是多少？

        （解答时须给出图示）                    

     解答

江苏卷

22.（本小题满分14分，第一小问满分4分，第二小问满分10分）

已知，函数

  ⑴当时，求使成立的的集合；

  ⑵求函数在区间上的最小值

解答

浙江卷(理)

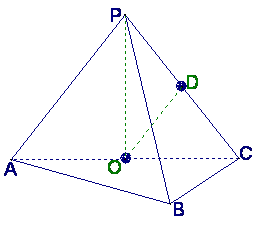
18．如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝kPA，点O、D分别是AC、PC的中点，

OP⊥底面ABC．

   (Ⅰ)当k＝时，求直线PA与平面PBC所成角的大小；

   (Ⅱ) 当k取何值时，O在平面PBC内的射影恰好

   为△PBC的重心？ 

解答

福建卷(理)

20．（本小题满分12分）

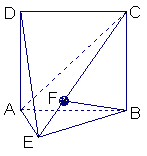
如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，

F为CE上的点，且BF⊥平面ACE.

（Ⅰ）求证AE⊥平面BCE；

 （Ⅱ）求二面角B—AC—E的大小；

 （Ⅲ）求点D到平面ACE的距离.

解答

湖北卷(理)

20．（本小题满分12分）

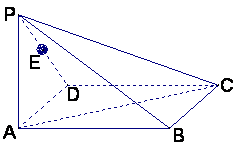如图，在四棱锥P—ABC右，底面ABCD为矩形，侧棱PA⊥底面ABCD，

AB=，BC=1，PA=2，E为PD的中点

（Ⅰ）求直线AC与PB所成角的余弦值；

（Ⅱ）在侧面PAB内找一点N，使NE⊥面PAC，

并求出N点到AB和AP的距离

解答

湖南卷(理)

19．（本小题满分14分）

已知椭圆C：＋＝1（a＞b＞0）的左．右焦点为F1、F2，离心率为e.

直线l：y＝ex＋a与x轴．y轴分别交于点A、B，M是直线l与椭圆C的一个公

共点，P是点F1关于直线l的对称点，设＝λ.

   （Ⅰ）证明：λ＝1－e2；

   （Ⅱ）确定λ的值，使得△PF1F2是等腰三角形.

解答

广东卷

18．（本小题满分12分）

箱中装有大小相同的黄、白两种颜色的乒乓球，黄、白乒乓球的数量比为s:t.

现从箱中每次任意取出一个球，若取出的是黄球则结束，若取出的是白球，则

将其放回箱中，并继续从箱中任意取出一个球，但取球的次数最多不超过n次，

以ξ表示取球结束时已取到白球的次数.

   （Ⅰ）求ξ的分布列；

   （Ⅱ）求ξ的数学期望.

解答

重庆卷(理)

20．（本小题满分13分）

    如图，在三棱柱ABC—A1B1C1中，AB⊥侧面BB1C1C，E为棱CC1上异于C、C1的一点，

    EA⊥EB1，已知AB=，BB1=2，BC=1，∠BCC1=，求：

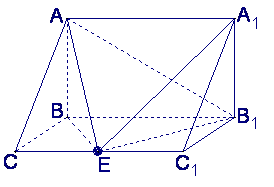   （Ⅰ）异面直线AB与EB1的距离；

   （Ⅱ）二面角A—EB1—A1的平面角的正切值.

  解

山东卷(理)

(20) （本小题满分12分）

如图，已知长方体，，直线与平面

所成的角为，垂直于为的中点．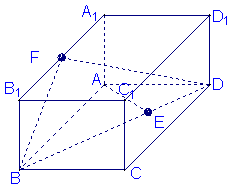

（Ⅰ）求异面直线与所成的角；

（Ⅱ）求平面与平面所成二面角（锐角）的大小；

（Ⅲ）求点到平面的距离 

解答

江西卷(理)

20．（本小题满分12分）

如图，在长方体ABCD—A1B1C1D1，中，AD=AA1=1，AB=2，点E在棱AB上移动.

   （1）证明：D1E⊥A1D；

   （2）当E为AB的中点时，求点E到面ACD1的距离；

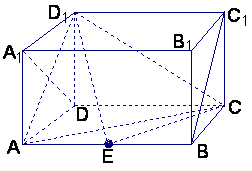   （3）AE等于何值时，二面角D1—EC—D的大小为.

      解答