解答题
全国卷Ⅰ(理)
(19)(本大题满分12分)
设等比数列![]() 的公比为
的公比为![]() ,前n项和
,前n项和![]()
![]()
(Ⅰ)求![]() 的取值范围;
的取值范围;
(Ⅱ)设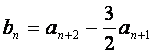 ,记
,记![]() 的前n项和为
的前n项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小
的大小![]()
全国卷Ⅱ(理)
(19)(本小题满分12分)
甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,
本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没
有影响.令![]() 为本场比赛的局数.求
为本场比赛的局数.求![]() 的概率分布和数学期望.(精确到0.0001)
的概率分布和数学期望.(精确到0.0001)
全国卷Ⅲ(理)
19.(本小题满分12分)
![]() 中,内角
中,内角![]() .
.![]() .
.![]() 的对边分别为
的对边分别为![]() .
.![]() .
.![]() ,已知
,已知![]() .
.![]() .
.![]() 成等比数列,且
成等比数列,且![]()
![]()
![]()
(1)求![]() 的值;
的值;
(2)若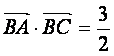 ,求
,求![]() 的值
的值![]()
北京卷(理)
17 (本小题共13分)
甲、乙俩人各进行3次射击,甲每次击中目标的概率为![]() ,乙每次击中目标的概率为
,乙每次击中目标的概率为![]()
![]()
(Ⅰ)记甲击中目标的次数为![]() ,求
,求![]() 的概率分布及数学期望
的概率分布及数学期望![]() ;
;
(Ⅱ)求乙至多击中目标2次的概率;
(Ⅲ)求甲恰好比乙多击中目标2次的概率![]()
天津卷(理)
(19)(本小题满分12分)
如图,在斜三棱柱![]() 中,
中,![]() ,
,
侧面![]() 与底面ABC所成的二面角为
与底面ABC所成的二面角为![]() ,E、F分别是棱
,E、F分别是棱![]() 的中点
的中点
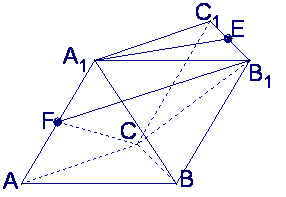 (Ⅰ)求
(Ⅰ)求![]() 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明![]() ∥平面
∥平面![]()
(Ⅲ)求经过![]() 四点的球的体积
四点的球的体积
上海卷(理)
19.点A、B分别是椭圆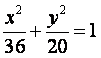 长轴的左、右焦点,点F是椭圆的右焦点
长轴的左、右焦点,点F是椭圆的右焦点![]() 点P在椭圆上,
点P在椭圆上,
且位于x轴上方,![]()
![]()
(1)求P点的坐标;
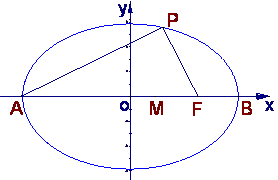 (2)设M是椭圆长轴AB上的一点,M到直线AP的
(2)设M是椭圆长轴AB上的一点,M到直线AP的
距离等于![]() ,求椭圆上的点到点M的距离d的最小值
,求椭圆上的点到点M的距离d的最小值![]()
辽宁卷
19.(本小题满分12分)
已知函数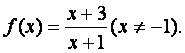 设数列
设数列![]() }满足
}满足![]() ,数列
,数列![]() }满足
}满足
![]()
(Ⅰ)用数学归纳法证明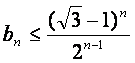 ;
;
(Ⅱ)证明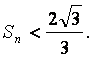
江苏卷
21.(本小题满分14分,第一小问满分6分,第二.第三小问满分各4分)
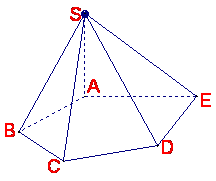 如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,
如图,在五棱锥S—ABCDE中,SA⊥底面ABCDE,SA=AB=AE=2,![]() ,
,
![]()
![]()
⑴求异面直线CD与SB所成的角(用反三角函数值表示);
⑵证明:BC⊥平面SAB;
⑶用反三角函数值表示二面角B—SC—D的大小![]() (本小问不必写出解答过程)
(本小问不必写出解答过程)
浙江卷(理)
17.如图,已知椭圆的中心在坐标原点,焦点![]() 在x轴上,长轴
在x轴上,长轴![]() 的长为4,
的长为4,
左准线![]() 与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
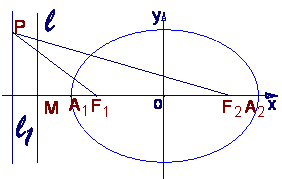 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线![]() :x=m(|m|>1),P为
:x=m(|m|>1),P为![]() 上的动点,
上的动点,
使![]() 最大的点P记为Q,求点Q的坐标(用m表示).
最大的点P记为Q,求点Q的坐标(用m表示).
福建卷(理)
19.(本小题满分12分)
已知函数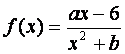 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
湖北卷(理)
19.(本小题满分12分)
某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有4次参加
考试的机会,一量某次考试通过,便可领取驾照,不再参加以后的考试,否则
就一直考到第4次为止![]() 如果李明决定参加驾照考试,设他每次参加考试通过的
如果李明决定参加驾照考试,设他每次参加考试通过的
概率依次为0.6,0.7,0.8,0.9![]() 求在一年内李明参加驾照考试次数
求在一年内李明参加驾照考试次数![]() 的分布列
的分布列
和![]() 的期望,并求李明在一所内领到驾照的概率
的期望,并求李明在一所内领到驾照的概率
湖南卷(理)
18.(本小题满分14分)
某城市有甲、乙、丙3个旅游景点,一位客人游览这三个景点的概率分别
是0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设ξ表示客人离开
该城市时游览的景点数与没有游览的景点数之差的绝对值.
(Ⅰ)求ξ的分布及数学期望;
(Ⅱ)记“函数f(x)=x2-3ξx+1在区间[2,+∞![]() 上单调递增”为
上单调递增”为
事件A,求事件A的概率.
广东卷
17.(本小题满分14分)
在平面直角坐标系xOy中,抛物线y=x2上异于坐标原点O的两不同动点A、B
满足AO⊥BO(如图4所示).
(Ⅰ)求△AOB的重心G(即三角形三条
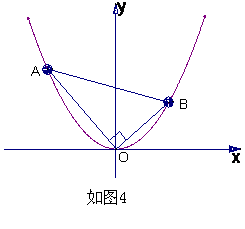
中线的交点)的轨迹方程;
(Ⅱ)△AOB的面积是否存在最小值?若存在,
请求出最小值;若不存在,请说明理由.
重庆卷(理)
19.(本小题满分13分)
已知![]() ,讨论函数
,讨论函数![]() 的极值点的个数
的极值点的个数![]()
山东卷(理)
(19) (本小题满分12分)
已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]()
![]() .
.
(Ⅰ)求m与n的关系表达式;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于3m,
的图象上任意一点的切线斜率恒大于3m,
求m的取值范围![]()
江西卷(理)
19.(本小题满分12分)
A、B两位同学各有五张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面
朝上时A赢得B一张卡片,否则B赢得A一张卡片.规定掷硬币的次数达9次时,或
在此前某人已赢得所有卡片时游戏终止.设![]() 表示游戏终止时掷硬币的次数.
表示游戏终止时掷硬币的次数.
(1)求![]() 的取值范围;
的取值范围;
(2)求![]() 的数学期望E
的数学期望E![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。