解答题

全国卷Ⅰ(理)

（18）（本大题满分12分）

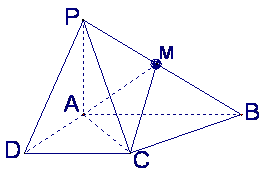
已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，底面ABCD，

且PA=AD=DC=AB=1，M是PB的中点

（Ⅰ）证明：面PAD⊥面PCD；

（Ⅱ）求AC与PB所成的角；

（Ⅲ）求面AMC与面BMC所成二面角的大小

解答

全国卷Ⅱ(理)

（18） （本小题满分12分）

已知是各项均为正数的等差数列，、、成等差数列．又，…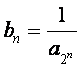

（Ⅰ）证明为等比数列；

（Ⅱ）如果无穷等比数列各项的和，求数列的首项和公差．

（注：无穷数列各项的和即当时数列前项和的极限）

解答

全国卷Ⅲ(理)

18.（本小题满分12分）

    四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，

    平面VAD⊥底面ABCD

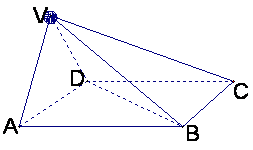    1）求证AB⊥面VAD；

    2）求面VAD与面VDB所成的二面角的大小．

   解答

北京卷(理)

16 (本小题共14分)

如图,在直四棱柱中,,

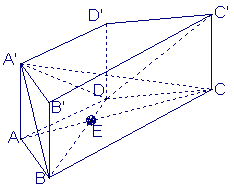
    垂足为

     (Ⅰ)求证;

     (Ⅱ)求二面角的大小;

     (Ⅲ)求异面直线与所成角的大小

 解答

天津卷(理)

（18）（本小题满分12分）

已知

 （Ⅰ）当时，求数列的前n项和

 （Ⅱ）求

  解答

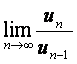
上海卷(理)

18.证明：在复数范围内，方程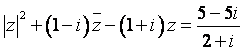（为虚数单位）无解

解答

辽宁卷

18．（本小题满分12分）

     如图，在直径为1的圆O中，作一关于圆心对称、

     邻边互相垂直的十字形，其中

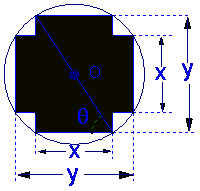
    （Ⅰ）将十字形的面积表示为的函数；

    （Ⅱ）为何值时，十字形的面积最大？最大面积是多少？

解答

江苏卷

20.（本小题满分12分，每小问满分4分）甲.乙两人各射击一次，

击中目标的概率分别是和假设两人射击是否击中目标，相互之间没有影响；

每人各次射击是否击中目标，相互之间也没有影响

⑴求甲射击4次，至少1次未击中目标的概率；

⑵求两人各射击4次，甲恰好击中目标2次且乙恰好击中目标3次的概率；

⑶假设某人连续2次未击中目标，则停止射击问：乙恰好射击5次后，被中止

射击的概率是多少？

解答

浙江卷(理)

16．已知函数f(x)和g(x)的图象关于原点对称，且f(x)＝x2＝2x．

   (Ⅰ)求函数g(x)的解析式；

   (Ⅱ)解不等式g(x)≥f(x)－|x－1|．

解答

福建卷(理)

18．（本小题满分12分）

甲、乙两人在罚球线投球命中的概率分别为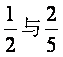，投中得1分，投不中得0分.

（Ⅰ）甲、乙两人在罚球线各投球一次，求两人得分之和ξ的数学期望；

（Ⅱ）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率；

解答

湖北卷(理)

18．（本小题满分12分）

在ΔABC中，已知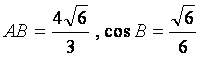，AC边上的中线BD=，求sinA的值

解答

湖南卷(理)

17．（本题满分12分）

　  如图1，已知ABCD是上．下底边长分别为2和6，高为的等腰梯形，

    将它沿对称轴OO1折成直二面角，如图2.

　　（Ⅰ）证明：AC⊥BO1；

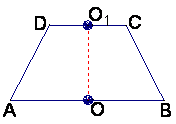
 （Ⅱ）求二面角O－AC－O1的大小.

       解答                                               图1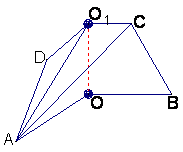                 图2

广东卷

16．（本小题满分14分）

如图3所示，在四面体P—ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=.

F是线段PB上一点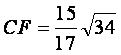，，点E在线段AB上，且EF⊥PB.

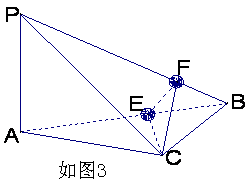   （Ⅰ）证明：PB⊥平面CEF；

   （Ⅱ）求二面角B—CE—F的大小.

解答

重庆卷(理)

18．（本小题满分13分）

在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；

有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券

中任抽2张，求：

    （Ⅰ）该顾客中奖的概率；

    （Ⅱ）该顾客获得的奖品总价值（元）的概率分布列和期望

解答

山东卷(理)

(18) （本小题满分12分）

袋中装有罴球和白球共7个,从中任取2个球都是白球的概率为.现有甲、乙

两人从袋中轮流摸取1个球，甲先取，乙后取，然后甲再取取后不放回，

直到两人中有一人取到白球时即终止 每个球在每一次被取出的机会是等可能的，

用表示取球终止时所需的取球次数．

（Ⅰ）求袋中原有白球的个数；

（Ⅱ）求随机变量的概率分布；

（Ⅲ）求甲取到白球的概率

解答

江西卷(理)

18．（本小题满分12分）

已知向量.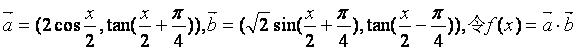

是否存在实数

若存在，则求出x的值；若不存在，则证明之.

解答