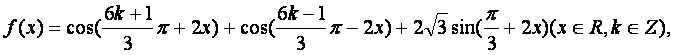
解答题
15．（本小题满分12分）
化简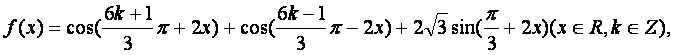
并求函数
的值域和最小正周期.
16．（本小题满分14分）
如图3所示，在四面体P—ABC中，已知PA=BC=6，PC=AB=10，AC=8，PB=
.
F是线段PB上一点，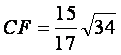
，点E在线段AB上，且EF⊥PB.
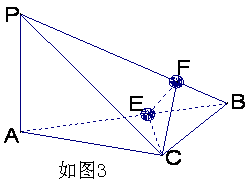（Ⅰ）证明：PB⊥平面CEF；
（Ⅱ）求二面角B—CE—F的大小.
17．（本小题满分14分）
在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A、B
满足AO⊥BO（如图4所示）.
（Ⅰ）求△AOB的重心G（即三角形三条
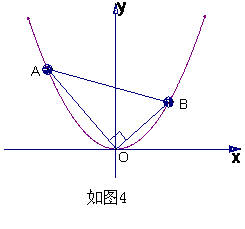
中线的交点）的轨迹方程；
（Ⅱ）△AOB的面积是否存在最小值？若存在，
请求出最小值；若不存在，请说明理由.
18．（本小题满分12分）
箱中装有大小相同的黄、白两种颜色的乒乓球，黄、白乒乓球的数量比为s:t.
现从箱中每次任意取出一个球，若取出的是黄球则结束，若取出的是白球，则
将其放回箱中，并继续从箱中任意取出一个球，但取球的次数最多不超过n次，
以ξ表示取球结束时已取到白球的次数.
（Ⅰ）求ξ的分布列；
（Ⅱ）求ξ的数学期望.
19．（本小题满分14分）
设函数
，
且在闭区间[0，7]上，只有
（Ⅰ）试判断函数
的奇偶性；
（Ⅱ）试求方程
在闭区间[－2005，2005]上的根的个数，并证明你的结论.
20．（本小题满分14分）
在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、
y轴的正半轴上，A点与坐标原点重合（如图5所示）.将矩形折叠，使A点落
在线段DC上.
（Ⅰ）若折痕所在直线的斜率为k，
试写出折痕所在直线的方程；
（Ⅱ）求折痕的长的最大值.
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。