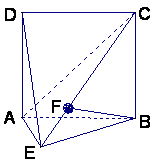
 如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,解答题
21.(本小题满分12分)
 如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,
F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
(Ⅲ)求点D到平面ACE的距离.
本题主要考查直线、直线和平面基点和平面的距离等基础知识,考察空间
想象能力,逻辑思维能力和运算能力![]()
(I)![]()
![]()
![]()
![]()
(II)连结AC、BD交于G,连结FG,∵ABCD为正方形,∴BD⊥AC,
∵BF⊥平面ACE,∴FG⊥AC,∠FGB为二面角B-AC-E的平面角,
由(I)可知,AE⊥平面BCE,∴AE⊥EB,又AE=EB,AB=2,AE=BE=![]() ,
,
在直角三角形BCE中,CE=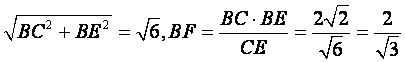
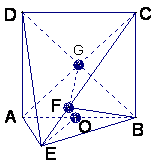 在正方形中,BG=
在正方形中,BG=![]() ,在直角三角形BFG中,
,在直角三角形BFG中,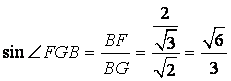
∴二面角B-AC-E为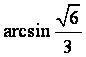
![]()
(III)由(II)可知,在正方形ABCD中,BG=DG,D到平面ACB的距离
等于B到平面ACE的距离,BF⊥平面ACE,线段BF的长度就是点B到平面ACE
的距离,即为D到平面ACE的距离![]() 所以D到平面的距离为
所以D到平面的距离为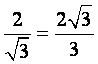
![]()
另法:过点E作![]() 交AB于点O.
OE=1.
交AB于点O.
OE=1.
∵二面角D—AB—E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,
![]()
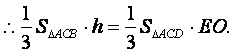
![]() 平面BCE,
平面BCE,![]()
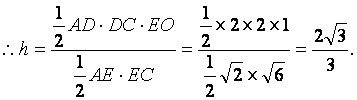
∴点D到平面ACE的距离为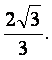
解法二:
(Ⅰ)同解法一.
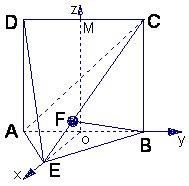
(Ⅱ)以线段AB的中点为原点O,OE所在直线为x轴,AB所在直线为y轴,
过O点平行于AD的直线为z轴,建立空间直角坐标系O—xyz,如图.
![]() 面BCE,BE
面BCE,BE![]() 面BCE,
面BCE, ![]() ,
,
在![]() 的中点,
的中点,
![]()
![]() 设平面AEC的一个法向量
设平面AEC的一个法向量
为![]() ,
,
 则
则
解得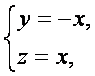
令![]() 得
得![]() 是平面AEC的一个法向量.
是平面AEC的一个法向量.
又平面BAC的一个法向量为![]() ,
,
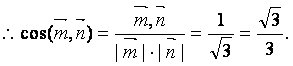
∴二面角B—AC—E的大小为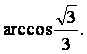
(III)∵AD//z轴,AD=2,∴![]() ,
,
∴点D到平面ACE的距离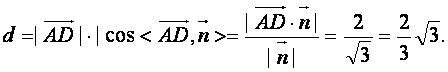
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。