解答题

17．（本小题满分12分）

已知.

（I）求sinx－cosx的值；

（Ⅱ）求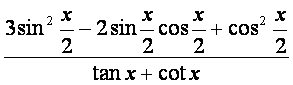的值.

解答

18．（本小题满分12分）

甲、乙两人在罚球线投球命中的概率分别为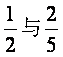，投中得1分，投不中得0分.

（Ⅰ）甲、乙两人在罚球线各投球一次，求两人得分之和ξ的数学期望；

（Ⅱ）甲、乙两人在罚球线各投球二次，求这四次投球中至少一次命中的概率；

解答

19．（本小题满分12分）

已知函数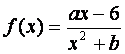的图象在点M（－1，f(x)）处的切线方程为x+2y+5=0.

 （Ⅰ）求函数y=f(x)的解析式；

 （Ⅱ）求函数y=f(x)的单调区间.

解答

20．（本小题满分12分）

如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，

F为CE上的点，且BF⊥平面ACE.

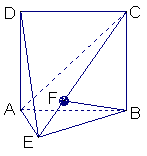（Ⅰ）求证AE⊥平面BCE；

 （Ⅱ）求二面角B—AC—E的大小；

 （Ⅲ）求点D到平面ACE的距离.

解答

21．（本小题满分12分）

已知方向向量为v=(1,)的直线l过点（0，－2）和

椭圆C：的焦点，且椭圆C的中心关于直线l的对称点

在椭圆C的右准线上.

（Ⅰ）求椭圆C的方程；

（Ⅱ）是否存在过点E（－2，0）的直线m交椭圆C于点M、N，

满足cot∠MON≠0（O为原点）.若存在，求直线m的方程；

若不存在，请说明理由.

            解答

22．（本小题满分14分）

已知数列{an}满足a1=a, an+1=1+我们知道当a取不同的值时，得到不同

的数列，如当a=1时，得到无穷数列：

（Ⅰ）求当a为何值时a4=0；

（Ⅱ）设数列{bn­}满足b1=－1, bn+1=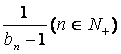，求证a取数列{bn}中的

任一个数，都可以得到一个有穷数列{an}；

（Ⅲ）若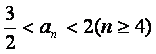，求a的取值范围.

解答