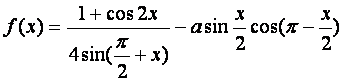解答题

17．（本小题满分13分）

       若函数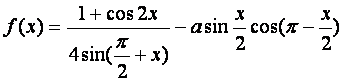的最大值为2，试确定常数a的值.

解答

18．（本小题满分13分）

在一次购物抽奖活动中，假设某10张券中有一等奖券1张，可获价值50元的奖品；

有二等奖券3张，每张可获价值10元的奖品；其余6张没有奖，某顾客从此10张券

中任抽2张，求：

    （Ⅰ）该顾客中奖的概率；

    （Ⅱ）该顾客获得的奖品总价值（元）的概率分布列和期望

解答

19．（本小题满分13分）

       已知，讨论函数的极值点的个数

解答

20．（本小题满分13分）

    如图，在三棱柱ABC—A1B1C1中，AB⊥侧面BB1C1C，E为棱CC1上异于C、C1的一点，

    EA⊥EB1，已知AB=，BB1=2，BC=1，∠BCC1=，求：

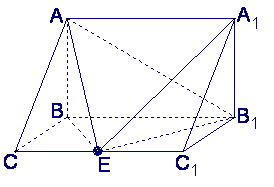   （Ⅰ）异面直线AB与EB1的距离；

   （Ⅱ）二面角A—EB1—A1的平面角的正切值.

  解

21．（本小题满分12分）

    已知椭圆C1的方程为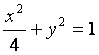，双曲线C2的左、右焦点分别为C1的左、右顶点，

    而C2的左、右顶点分别是C1的左、右焦点.

    （Ⅰ）求双曲线C2的方程；

  （Ⅱ）若直线与椭圆C1及双曲线C2都恒有两个不同的交点，且l与C2

  的两个交点A和B满足（其中O为原点），求k的取值范围.

 解答

22．（本小题满分12分）

       数列{an}满足.

    （Ⅰ）用数学归纳法证明：；

  （Ⅱ）已知不等式，其中无理数

e=2.71828….

解答