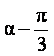 )的值.
)的值.解答题
17.已知0<α<![]() ,tan
,tan![]() +cot
+cot![]() =
=![]() ,求sin(
,求sin(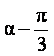 )的值.
)的值.
18.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,
点P在棱CC1上,且CC1=4CP.
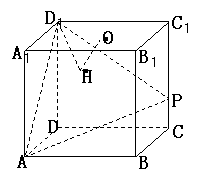 (Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);
(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);
(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;
(Ⅲ)求点P到平面ABD1的距离.
19.制定投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.
某投资人打算投资甲、乙两个项目. 根据预测,甲、乙项目可能的最大
盈利率分别为100﹪和50﹪,可能的最大亏损分别为30﹪和10﹪. 投资人计
划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元. 问投
资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
20.设无穷等差数列{an}的前n项和为Sn.
(Ⅰ)若首项![]() EQ \F(3,2)
,公差
EQ \F(3,2)
,公差![]() ,求满足
,求满足![]() 的正整数k;
的正整数k;
(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有![]() 成立.
成立.
21.已知椭圆的中心在原点,离心率为 EQ \F(1,2) ,一个焦点是F(-m,0)
(m是大于0的常数).
(Ⅰ)求椭圆的方程;
(Ⅱ)设Q是椭圆上的一点,且过点F、Q的直线![]() 与y轴交于点M.
若
与y轴交于点M.
若![]() ,
,
求直线![]() 的斜率.
的斜率.
22.已知函数![]() 满足下列条件:对任意的实数x1,x2都有
满足下列条件:对任意的实数x1,x2都有
![]() 和
和![]() ,其中
,其中![]() 是大于0的常数.
是大于0的常数.
设实数a0,a,b满足
![]() 和
和![]()
(Ⅰ)证明![]() ,并且不存在
,并且不存在![]() ,使得
,使得![]() ;
;
(Ⅱ)证明![]() ;
;
(Ⅲ)证明![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。