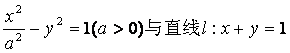 相交于两个不同的点A、B.
相交于两个不同的点A、B.解答题
全国卷Ⅰ(文)
22.(本小题满分14分)
设双曲线C: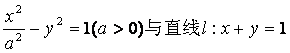 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围:
(II)设直线l与y轴的交点为P,且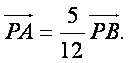 求a的值.
求a的值.
全国卷Ⅱ(文)
22.(本小题满分14分)
给定抛物线C:![]() F是C的焦点,过点F的直线
F是C的焦点,过点F的直线![]() 与C相交于A、B两点.
与C相交于A、B两点.
(Ⅰ)设![]() 的斜率为1,求
的斜率为1,求![]() 夹角的大小;
夹角的大小;
(Ⅱ)设![]() ,求
,求![]() 在
在![]() 轴上截距的变化范围.
轴上截距的变化范围.
全国卷Ⅲ(文)
22.(本小题满分12分)设椭圆 的两个焦点是
的两个焦点是![]() 与
与![]() ,
,
且椭圆上存在一点![]() ,使得直线
,使得直线![]() 与
与![]() 垂直.
垂直.
(1)求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是相应于焦点
是相应于焦点![]() 的准线,直线
的准线,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若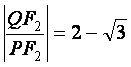 ,
,
求直线![]() 的方程.
的方程.
全国卷Ⅳ(文)
22.(本小题满分14分)
双曲线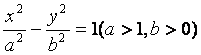 的焦距为2c,直线
的焦距为2c,直线![]() 过点(a,0)和(0,b),
过点(a,0)和(0,b),
且点(1,0)到直线![]() 的距离与点(-1,0)到直线
的距离与点(-1,0)到直线![]() 的距离之和
的距离之和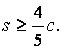 求双
求双
曲线的离心率e的取值范围.
天津卷(文)
22.(本小题满分14分)
椭圆的中心是原点O,它的短轴长为![]() ,相应于焦点
,相应于焦点![]()
![]() 的
的
准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,过点A的直线与椭圆相交于P、Q两点。
,过点A的直线与椭圆相交于P、Q两点。
(1)求椭圆的方程及离心率;(2)若![]() ,求直线PQ的方程。
,求直线PQ的方程。
辽宁卷
22.(本小题满分12分)
已知函数![]() .
.
(1)求函数![]() 的反函数
的反函数![]() 的导数
的导数![]()
(2)假设对任意![]() 成立,求实
成立,求实
数m的取值范围.
江苏卷
22.已知函数![]() 满足下列条件:对任意的实数x1,x2都有
满足下列条件:对任意的实数x1,x2都有
![]() 和
和![]() ,其中
,其中![]() 是大于0的常数.
是大于0的常数.
设实数a0,a,b满足
![]() 和
和![]()
(Ⅰ)证明![]() ,并且不存在
,并且不存在![]() ,使得
,使得![]() ;
;
(Ⅱ)证明![]() ;
;
(Ⅲ)证明![]() .
.
浙江卷(文)
(22)(本题满分14分)
解:已知双曲线的中心在原点,右顶点为A(1,0)点P、Q在双
曲线的右支上,支M(m,0)到直线AP的距离为1。
(Ⅰ)若直线AP的斜率为k,且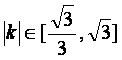 ,求实数m的
,求实数m的
取值范围;
(Ⅱ)当![]() 时,ΔAPQ的内心恰好是点M,求此双曲
时,ΔAPQ的内心恰好是点M,求此双曲
线的方程。
福建卷(文)
22.(本小题满分14分)
已知f(x)=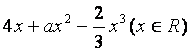 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:
的两个非零实根为x1、x2.试问:
是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
湖北卷(文)
22.(本小题满分14分)
已知![]() 的图象相切.
的图象相切.
(Ⅰ)求b与c的关系式(用c表示b);
(Ⅱ)设函数![]() 内有极值点,求c的取值范围.
内有极值点,求c的取值范围.
湖南卷(文)
22.(本小题满分14分)
如图,过抛物线x2=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线
交于A,B两点,点Q是点P关于原点的对称点。
(I)设点P分有向线段![]() 所成的比为
所成的比为![]() ,证明:
,证明:![]()
![]()
(II)设直线AB的方程是x-2y+12=0,过A,B两点的圆C与抛物线在点A处有
共同的切线,求圆C的方程.
重庆卷(文)
22.(本小题满分14分)
设数列![]() 满足:
满足:![]()
(1)
令![]() 求数列
求数列![]() 的通项公式;
的通项公式;
(2)
求数列![]() 的前n项和
的前n项和![]() 。
。
北京卷(文)
(20)(本小题满分12分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275。现将
这些数按下列要求进行分组, 每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和
的差![]() 与所有可能的其他选择
相比是最小的,
与所有可能的其他选择
相比是最小的,![]() 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构
成第二组,这时的余差为![]() ;
如此继续构成第三组(余差为
;
如此继续构成第三组(余差为![]() )、第四组
)、第四组
(余差为![]() )、……,直至第N组(余差为
)、……,直至第N组(余差为![]() )把这些数全部分
完为止。
)把这些数全部分
完为止。
(I)判断![]() 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n<N)组后,指出余下的每个数与![]() 的大小关系,并证明
的大小关系,并证明
![]()
(III)对任何满足条件T的有限个正数,证明:![]()
上海卷(文)
22、(本题满分18分) 第1小题满分6分, 第2小题满分4分, 第3小题满分8分
设P1(x1,y1), P1(x2,y2),…, Pn(xn,yn)(n≥3,n∈N) 是二次曲线C上的点,
且a1=![]() 2,
a2=
2,
a2=![]() 2,
…, an=
2,
…, an=![]() 2构成了一个公差为d(d≠0)
的等差数列,
2构成了一个公差为d(d≠0)
的等差数列,
其中O是坐标原点. 记Sn=a1+a2+…+an.
(1)
若C的方程为![]() -y2=1,n=3.
点P1(3,0)
及S3=162,
求点P3的坐标;
-y2=1,n=3.
点P1(3,0)
及S3=162,
求点P3的坐标;
(只需写出一个)
(2) 若C的方程为y2=2px(p≠0). 点P1(0,0), 对于给定的自然数n, 证明:
(x1+p)2, (x2+p)2, …,(xn+p)2成等差数列;
(3)
若C的方程为![]() (a>b>0).
点P1(a,0),
对于给定的自然数n,
当
(a>b>0).
点P1(a,0),
对于给定的自然数n,
当
公差d变化时, 求Sn的最小值.
广东卷
22.(14分)设直线![]() 与椭圆
与椭圆![]() 相交于A、B两点,
相交于A、B两点,![]() 又与双曲线x2–y2=1
又与双曲线x2–y2=1
相交于C、D两点,
C、D三等分线段AB. 求直线![]() 的方程.
的方程.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。