解答题

17．（本小题满分12分）

       求函数的取小正周期和取小值；

并写出该函数在上的单调递增区间。

解答

18．（本小题满分12分）

设一汽车在前进途中要经过4个路口，汽车在每个路口遇到绿灯的

概率为，遇到红灯（禁止通行）的概率为。假定汽车只在遇到

红灯或到达目的地才停止前进，表示停车时已经通过的路口数，求：

（1）的概率的分布列及期望E;

 (2 )  停车时最多已通过3个路口的概率。

解答

19．（本小题满分12分） 

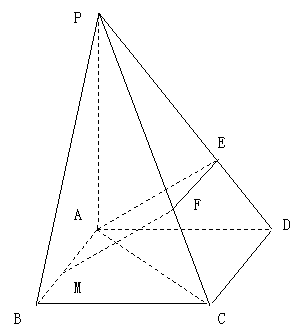
如图，四棱锥P-ABCD的底面是正方形，

(1)  证明MF是异面直线AB与PC的公垂线；

(2)  若,求直线AC与平面EAM所成角的正弦值。

解答

20．（本小题满分12分）

设函数

(1)    求导数; 并证明有两个不同的极值点;

(2) 若不等式成立，求的取值范围。

解答

21．（本小题满分12分）

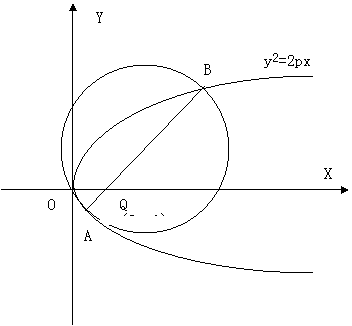
设是一常数，过点的直线与抛物线交于相异

两点A、B，以线段AB为直经作圆H（H为圆心）。试证抛物线顶点

在圆H的圆周上；并求圆H的面积最小时直线AB的方程。

22．（本小题满分14分）

      设数列满足

(1)     证明对一切正整数n 成立；

(2)  令,判断的大小，并说明理由。

解答