解答题

（20）（本小题满分13分）

    给定有限个正数满足条件T：每个数都不大于50且总和L＝1275。

现将这些数按下列要求进行分组，每 组数之和不大于150且分组的步骤是：

    首先，从这些数中选择这样一些数构成第一组，使得150与这组数之

和的差与所有可能的其他选择相 比是最小的，称为第一组余差；

    然后，在去掉已选入第一组的数后，对余下的数按第一组的选择方式

构成第二组，这时的余差为； 如此继续构成第三组（余差为）、第四组

（余差为）、……，直至第N组（余差为）把这些数全部分 完为止。

    （I）判断的大小关系，并指出除第N组外的每组至少含有几个数
   

    （II）当构成第n（n<N）组后，指出余下的每个数与的大小关系，

并证明

    （III）对任何满足条件T的有限个正数，证明：

本小题主要考查不等式的证明等基本知识，考查逻辑思维能力、分析问题和

解决问题的能力。满分13分。

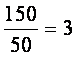    解：（I）。除第N组外的每组至少含有个数

    （II）当第n组形成后，因为，所以还有数没分完，这时余下的

每个数必大于余差，余下数之 和也大于第n组的余差，即

    由此可得

    因为，所以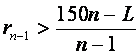

    （III）用反证法证明结论，假设，即第11组形成后，还有数

没分完，由（I）和（II）可知， 余下的每个数都大于第11组的余差，

且

    故余下的每个数    （*）

    因为第11组数中至少含有3个数，所以第11组数之和大于

    此时第11组的余差

    这与（*）式中矛盾，所以