浙江(理)
一、选择题(每小题5分)
(3)已知0<a<1,![]() m<
m<![]() n<0,则
n<0,则
(A)1<n<m (B)1<m<n
(C)![]() m<n<1 (D)n<m<1
m<n<1 (D)n<m<1
(4)在平面直角坐标系中,不等式组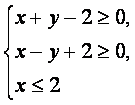 表示的平面区域的面积是()
表示的平面区域的面积是()
(A)![]() (B)4 (C)
(B)4 (C)![]() (D)2
(D)2
(7)“a>b>0”是“ab<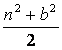 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
天津(理)
一、选择题(每小题5分)
(3)设变量x、y满足约束条件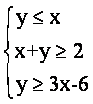 ,
则目标函数Z=2x+y的最小值为()
,
则目标函数Z=2x+y的最小值为()
(A)2 (B)3 (C)4 (D)9
江苏
一、选择题(每小题5分)
(8)设a、b、c是互不相等的正数,则下列等式中不恒成立的是()
(A)![]() (B)
(B)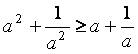
(C) (D)
(D)![]()
二、填空题(每小题5分)
(12)设变量x、y满足约束条件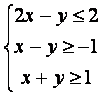 ,则
,则![]() 的最大值为
的最大值为
(16)不等式 的解集为
解答
的解集为
解答
重庆(理)
一、选择题(每小题5分)
(10)若![]() 且
且![]() ,则
,则![]() 的最小值为()
的最小值为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
湖南(理)
二、填空题(每题4分)
12.已知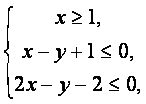 则x2+y2的最小值是
.
则x2+y2的最小值是
.
广东
一、选择题(每题5分)
9、在约束条件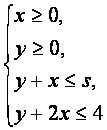 下,当3
下,当3![]() 5时,目标函数z=3x+2y的最大值
5时,目标函数z=3x+2y的最大值
的变化范围是( )
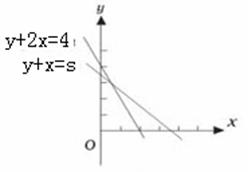
A、[6,15] B、[7,15]
C、[6,8] D、[7,8]
上海(理)
一、填空题(每小题4分)
12.三个同学对问题“关于![]() 的不等式
的不等式![]() +25+|
+25+|![]() -5
-5![]() |≥
|≥![]() 在[1,12]
在[1,12]
上恒成立,求实数![]() 的取值范围”提出各自的解题思路.
的取值范围”提出各自的解题思路.
甲说:“只须不等式左边的最小值不小于右边的最大值”.
乙说:“把不等式变形为左边含变量![]() 的函数,右边仅含常数,
的函数,右边仅含常数,
求函数的最值”.
丙说:“把不等式两边看成关于![]() 的函数,作出函数图像”.
的函数,作出函数图像”.
参考上述解题思路,你认为他们所讨论的问题的正确结论,即![]() 的取值
的取值
范围是 .解答
二、选择题(每小题4分)
15.若关于![]() 的不等式
的不等式![]() ≤
≤![]() +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数![]() ,
,
总有[答]( )
(A)2∈M,0∈M;
(B)2![]() M,0
M,0![]() M;
(C)2∈M,0
M;
(C)2∈M,0![]() M;
(D)2
M;
(D)2![]() M,0∈M.
M,0∈M.
山东(理)
一、选择题(每小题5分)
3.设f(x)=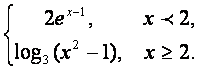 则不等式f(x)>2的解集为()
则不等式f(x)>2的解集为()
(A)(1,2)∪(3,+∞)
(B)(![]() ,+∞)
,+∞)
(C)(1,2)∪(![]() ,+∞)
(D)(1,2)
,+∞)
(D)(1,2)
11.某公司招收男职员x名,女职员y名,x和y须满足约束条件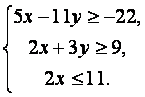
则z=10x+lOy的最大值是()
(A)80 (B)85 (C)90 (D)95
江西(理)
一、选择提(每题5分)
3.若a>0,b>0则不等式-b<![]() <a等价于(
)
<a等价于(
)
A.-![]() <x<0或0<x<
<x<0或0<x<![]() B.-
B.-![]() <x<
<x<![]()
C. x<-![]() 或x>
或x>![]() D. x<-
D. x<-![]() 或x>
或x>![]()
5.对于R上可导的任意函数f(x),若满足(x-1)f′(x)≥0,则必有( )
A.f(0)+f(2)<2f(1) B.f(0)+f(2)≤2f(1)
C. f(0)+f(2)≥2f(1) D.f(0)+f(2)>2f(1)
6.若不等式x2+ax+l≥0对一切x∈(0,![]()
![]() 成立,则a的最小值为
( )
成立,则a的最小值为
( )
A.0
B.-2 C.-![]() D.-3
D.-3
陕西(理)
一、选择题(每小题5分)
8.已知不等式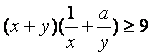 对任意正实数
对任意正实数![]() 恒成立,则正实数
恒成立,则正实数![]() 的最
的最
小值为
(A)8 (B)6 (C)4 (D)2
安徽(理)
一、选择题(每题5分)
(4)设![]() :(
:(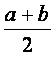 )2
)2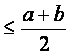 ,则p则q成立的(
)
,则p则q成立的(
)
(A)必要不充分条件 (B)充分不必要条件
(C)充分必要条件 (D)既不充分也不必要条件
(10)如果实数![]() 、
、![]() 满足条件
满足条件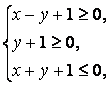 那么2
那么2![]() 的最大值为(
)
的最大值为(
)
(A)2 (B)1 (C)-2 (D)-3
全国卷(Ⅰ)理
二、填空题(每题5分)
(14)设![]() ,式中变量x、y满足下列条件
,式中变量x、y满足下列条件
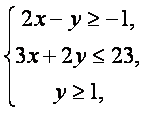
则z的最大值为 。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。