三、解答题

(19)如图，椭圆 (a＞b＞0)与过点A(2，0)、B(0，1)的直线有

且只有一个公共点T，且椭圆的离心率e=

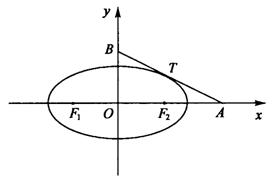
    (Ⅰ)求椭圆方程；

    (Ⅱ)设F_l、F₂分别为椭圆的左、右焦点，求证：|AT|²=|AF₁|·|AF₂|．

本题主要考查直线与椭圆的位置关系、椭圆的几何性质，考查解析几何的

基本思想方法和综合解题能力。满分14分。

  解：（Ⅰ）过A、B的直线方程为

因为由题意得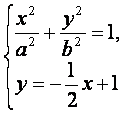有惟一解，

即（b²+）x²-a²x+a²-a²b²=0有惟一解，

所以

Δ=a²b² (a²+4b²-4)=0(ab≠0),

故a²+4b²-4=0.

又因为e=即

所以a²=4b².

从而得a²=2，b²=，

故所需求的椭圆的方程为

（Ⅱ）由（Ⅰ）得c=

     所以F₁（-，0），F₂（，0）.

         由解得x₁=x₂=1，

     因此T（1，）.

     从而|AT|²=

     因为|AF₁|·|AF₂|=，

     所以|AT|²=|AF₁|·|AF₂|.