一、选择题（每小题5分）

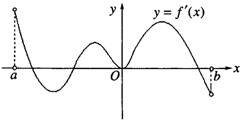
(9)函数f(x)的定义域为开区间(a,b)，导函数f′(x)在(a，b)内的图象

如图所示，则函数f(x)在开区间(a，b)内有极小值点（）

                           (A)1个

    (B)2个

    (C)3个

    (D)4个

解答

(10)已知函数y=f(x)的图象与函数y=a^x(a＞0且a=1)的图象关于直线y=x对称，

记g(x)=f(x)［f(x)+f(2)-1］．若y=g(x)在区间[，2]上是增函数，

则实数a的取值范围是（）

 (A)[2，+∞)  (B)(0，1)∪(1，2)    (C)[，1)      (D)(0，]

解答

二、填空题（每小题4分）

(15)某公司一年购买某种货物400吨，每次都购买x吨，运费为4万元／次，

—年的总存储费用为4x万元，要使—年的总运费与总存储费用之和最小，

则x=___________吨．解答

(16)设函数f(x)=,点A₀表示坐标原点，点A_n(n，f(n))(n∈N^*).若向量

θ_n是与的夹角(其中=(1，0))，

设S_n=tanθ_l+tanθ₂+…+tanθ_n，则S_n=_____________.解答

三、解答题

 (20)(本小题满分12分)

    已知函数f(x)=4x³-3x²cosθ+cosθ，其中x∈R,θ为参数，且0≤θ＜2π．

    (Ⅰ)当cosθ=0时，判断函数f(x)是否有极值；

    (Ⅱ)要使函数f(x)的极小值大于零，求参数θ的取值范围；

    (Ⅲ)若对(Ⅱ)中所求的取值范围内的任意参数θ，函数f(x)在区间

(2a-1，a)内都是增函数，求实数α的取值范围．

解答