三、解答题

21.(本题满分16分)本题共有3个小题，第4小题满分4分.第2小题满分5分，

第3小题满分7分.

已知在平面直角坐标系xOy中的一个椭圆，它的中心在原点，左焦点为

F（-，0）.且右顶点为D（2，0），设点A的坐标是（1，）.

(1)求该椭圆的标准方程.

(2)若P是椭圆上的动点，求线段PA中点M的轨迹方程；

(3)过原点O的直线交椭圆于点B、C.求△ABC面积的最大值.

解(1)由已知得椭圆的半长轴a=2,半焦距c=,则半短轴b=1.

     又椭圆的焦点在x轴上, ∴椭圆的标准方程为

(2)设线段PA的中点为M(x,y) ,点P的坐标是(x₀,y₀),

由  得 

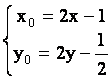
点P在椭圆上,得,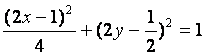

∴线段PA中点M的轨迹方程是.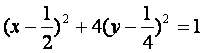

(3)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S_△ABC=1.

当直线BC不垂直于x轴时,说该直线方程为y=kx,代入,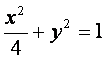

解得B(,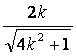),C(－,－),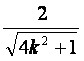

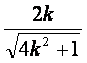则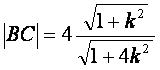,又点A到直线BC的距离d=,

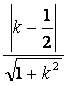∴△ABC的面积S_△ABC=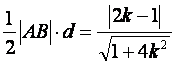

于是S_△ABC=

由≥－1,得S_△ABC≤,其中,当k=－时,等号成立.

∴S_△ABC的最大值是.