三、解答题

20(本题满分14分)本题共有2个小题，第1小题满分7分，第2小题满分7分.

设数列{a_n}的前n项和为S_n，且对任意正整数n，a_n+S_n=4096.

(1)求数列{a_n}的通项公式：

(2)设数列{log₂a_n}的前n项和为T_n.对数列{T_n}，从第几项起T_n＜-509？

解(1) ∵a_n+ S_n=4096, ∴a₁+ S₁=4096, a₁ =2048.

     当n≥2时, a_n= S_n－S_n－1=(4096－a_n)－(4096－a_n－1)= a_n－1－a_n

       ∴=     a_n=2048()^n－1.

     (2) ∵log₂a_n=log₂[2048()^n－1]=12－n,

     ∴T_n=(－n²+23n).

     由T_n<－509,解待n>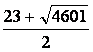,而n是正整数,于是,n≥46.

     ∴从第46项起T_n<－509.