三、解答题

（21）（本小题满分12分）

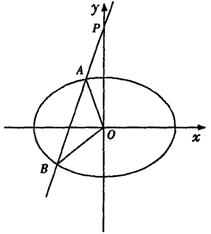
已知椭圆的中心在坐标原点O，焦点在x轴上，椭圆的短轴端点和焦点

所组成的四边形为正方形，两准线间的距离为4.

(Ⅰ)求椭圆的方程；

(Ⅱ)直线l过点P(0,2)且与椭圆相交于A、B两点，当ΔAOB面积取得最大值时，

求直线l的方程.

解：设椭圆方程为＝1(a＞b＞0)．

(Ⅰ)由已知得        .

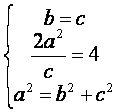
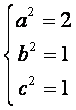    ∴所求椭圆方程为

      +y²=1．

(Ⅱ)解法一：由题意知直线l的斜率存在，

            设直线l的方程为y=kx+2，A(x₁，y₁)，B(x₂，y₂)，

    由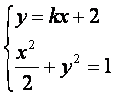，消去y得关于x的方程：

    (1+2k²)x²+8kx+6＝0，

    由直线l与椭圆相交于A、B两点，∴△＞0  64k²-24(1+2k²)＞0，

    解得  k²＞，

   又由韦达定理得   

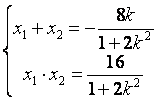
  ∴|AB|＝|x₁-x₂|＝

        ＝

    原点O到直线l的距离d=.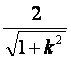

    ∴S_△AOB=|AB|·d=．

    解法1：对S=两边平方整理得：

    4S²k⁴+4(S²-4)k²+S²+24=0                    (*)

∵S≠0，

∴

    整理得：S²≤.

    又S＞0，

    ∴0＜S≤.

    从而S_△AOB的最大值为S=，

    此时代入方程(*)得

    4k⁴-28k²+49＝0

    ∴k=±

    所以，所求直线方程为：±x-2y+4＝0．

解法2：令m=(m＞0)，

       则2k²=m²+3.

       ∴S=≤.

    当且仅当m＝即m＝2时，

    S_max=.

    此时k=±.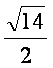

    所以，所求直线方程为±x-2y+4＝0．

解法二：由题意知直线l的斜率存在且不为零．

    设直线l的方程为y＝kx+2，A(x₁，y₁)，B(x₂，y₂)，

    则直线l与x轴的交点D(-，0)，

由解法一知    k²＞且    

    解法1：S_△AOB=|OD|·|y₁-y₂|=||·|kx₁+2-kx₂-2|

               ＝|x₁-x₂|

＝

    =

    =.

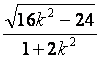
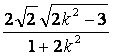   下同解法一.

解法2：S_△AOB=S_△POB-S_△POA

    =×2×||x₂|-|x₁||

    =|x₂-x₁|

    =.

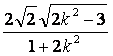    下同解法一．