18.(本小题满分12分)
已知函数F(x)=Asin2(ωx+φ)(A>0,ω>0,0<φ<![]() ),且y=f(x)的最大值为2,
),且y=f(x)的最大值为2,
其图象相邻两对称轴间的距离为2,并过点(1,2).
(Ⅰ)求φ;
(Ⅱ)计算f(1)+f(2)+…+f(2008).
解:(Ⅰ)y=![]() Asin2(ωx+φ)=
Asin2(ωx+φ)=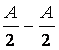 cos(2ωx+2φ).
cos(2ωx+2φ).
∵y=f(x)的最大值为2,![]() >0,
>0,
∴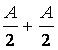 =2,
=2,![]() =2.
=2.
又∵其图象相邻两对称轴间的距离为2,ω>0,
∴![]() =2,ω=
=2,ω=![]() .
.
∴f(x)= cos(
cos(![]() +2φ)=1-cos(
+2φ)=1-cos(![]() +2φ).
+2φ).
∵y=f(x)过(1,2)点,
∴cos(![]() +2φ)=-1.
+2φ)=-1.
∴![]() +2φ=2kπ+π,k∈Z,
+2φ=2kπ+π,k∈Z,
∴2φ=2kπ+![]() ,k∈Z,
,k∈Z,
∴φ=kπ+![]() ,k∈Z.
,k∈Z.
又∵0<φ<![]() ,
,
∴φ=![]() .
.
(Ⅱ)解法一:∵φ=![]() ,
,
∴y=1-cos(![]() x+
x+![]() )=1+sin
)=1+sin![]() x.
x.
∴f(1)+f(2)+f(3)+f(4)=2+1+0+1=4.
又∵y=f(x)的周期为4,2008=4×502.
∴f(1)+f(2)+…+f(2008)=4×502=2008.
解法二:∵f(x)=2sin2(![]() x+φ)
x+φ)
∴f(1)+f(3)=2sin2(![]() +φ)+2sin2(
+φ)+2sin2(![]() +φ)=2,
+φ)=2,
f(2)+f(4)=2sin2(![]() +φ)+2sin2(π+φ)=2,
+φ)+2sin2(π+φ)=2,
∴f(1)+f(2)+f(3)+f(4)=4.
又y=f(x)的周期为4,2008=4×502.
∴f(1)+f(2)+…+f(2008)=4×502=2008.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。