一、选择题（每小题5分）

1.定义集合运算：A⊙B={z|z=xy(x+y)，x∈A，y∈B}．设集合A={0，1}，

B={2，3}，则集合A⊙B的所有元素之和为（）

   (A)0            (B)6                  (C)12                 (D)18

 解答

5.设向量a=(1，-3)，b=(-2，4)，c=(-1，-2)．若表示向量4a、4b-2c、2(a-c)、d

的有向线段首尾相接能构成四边形，则向量d为（）

   (A)(2，6)                           (B)(-2，6)

   (C)(2，-6)                          (D)(-2，-6)

解答

9.已知集合A＝{5}，B＝{1，2}，C={1,3，4}，从这三个集合中各取一个元素

构成空间直角坐标系中点的坐标，则确定的不同点的个数为（）

  (A)33          (B)34              (C)35                 (D)36

解答

二、填空题（每小题4分）

13.若=1，则常数a=________. 解答

16.下列四个命题中，真命题的序号有________(写出所有真命题的序号)．

   ①将函数y=|x+1|的图象按向量v=(-1，0)平移，得到的图象对应的函数

表达式为y=|x|

   ②圆x²+y²+4x+2y+1=0与直线y=x相交，所得弦长为2

   ③若sin(α+β)=，sin(α-β)=，则tanαcotβ=5

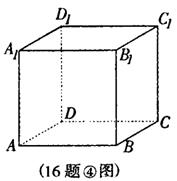
   ④如图，已知正方体ABCD-A₁B₁C₁D₁，P为底面ABCD内一动点，

P到平面AA₁D₁D的距离与到直线CC₁的距离相等，则P点的轨迹是

抛物线的一部分

解答